Pokrycie wierzchołkowe kontratakuje
W Delcie 7/2009 Marek Cygan opisał pewien sposób radzenia sobie z tym, że dla niektórych trudnych problemów nie potrafimy znaleźć szybkiego algorytmu. Autor rozważał klasę problemów NP-trudnych – czyli takich, których prawdopodobnie nie można rozwiązać w czasie wielomianowym – i pokazywał, że dla wielu z nich można w efektywny sposób skonstruować nie dokładne, lecz przybliżone rozwiązanie.
W tym artykule spróbujemy ugryźć trudne problemy z drugiej strony. Wciąż poruszamy się w świecie algorytmów działających w czasie wielomianowym – te uznajemy za szybkie. Ale zamiast poszukiwać dokładnego rozwiązania, użyjemy innej sztuczki: będziemy szukali algorytmów, które starają się jak najbardziej zmniejszyć rozmiar instancji (czyli egzemplarza problemu, np. zadanego grafu), zachowując przy tym odpowiedź. Wówczas, dla zredukowanej instancji, możemy odpalić nasz ulubiony algorytm dokładny, np. rozpatrujący wszystkie możliwości. A jako że rozmiar egzemplarza będzie dużo mniejszy od początkowego, algorytm dokładny być może zadziała całkiem szybko. Przejdźmy do przykładu.
Definicja. Pokryciem wierzchołkowym
w grafie
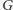 nazwiemy taki zbiór wierzchołków
nazwiemy taki zbiór wierzchołków
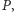 że każda
krawędź
że każda
krawędź
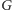 ma co najmniej jeden koniec w
ma co najmniej jeden koniec w
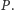
Problem znalezienia liczności najmniejszego pokrycia wierzchołkowego
w danym grafie jest NP-trudny. Marek Cygan w swoim artykule pokazywał, jak
szybko znaleźć pokrycie wierzchołkowe, które jest co najwyżej dwa razy
liczniejsze od optymalnego (czyli tzw.
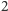 -aproksymację).
-aproksymację).
My będziemy rozważać wersję problemu pokrycia wierzchołkowego, w której
odpowiedź jest binarna („TAK” lub „NIE”). Mianowicie, mając dany graf
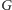 oraz liczbę naturalną
oraz liczbę naturalną
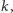 pytamy, czy w grafie
pytamy, czy w grafie
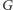 istnieje
pokrycie wierzchołkowe zawierające co najwyżej
istnieje
pokrycie wierzchołkowe zawierające co najwyżej
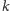 wierzchołków.
Oczywiście, z punktu widzenia algorytmów wielomianowych obie wersje są
równoważne: mając dany algorytm rozwiązujący wersję decyzyjną,
możemy wyszukać najmniejsze
wierzchołków.
Oczywiście, z punktu widzenia algorytmów wielomianowych obie wersje są
równoważne: mając dany algorytm rozwiązujący wersję decyzyjną,
możemy wyszukać najmniejsze
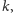 dla którego algorytm ten daje
odpowiedź „TAK”, i w ten sposób otrzymać rozmiar najmniejszego pokrycia
wierzchołkowego.
dla którego algorytm ten daje
odpowiedź „TAK”, i w ten sposób otrzymać rozmiar najmniejszego pokrycia
wierzchołkowego.
Mamy więc dany graf
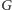 i liczbę
i liczbę
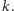 Co możemy teraz zrobić?
Ustalmy wierzchołek
Co możemy teraz zrobić?
Ustalmy wierzchołek
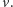 Jeśli
Jeśli
 nie należy do pewnego pokrycia
wierzchołkowego
nie należy do pewnego pokrycia
wierzchołkowego
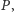 to wszyscy sąsiedzi
to wszyscy sąsiedzi
 muszą należeć do
muszą należeć do
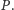 Poszukujemy
Poszukujemy
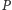 o mocy co najwyżej
o mocy co najwyżej
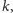 więc
jeśli
więc
jeśli
 ma co najmniej
ma co najmniej
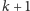 sąsiadów, to musimy wziąć
sąsiadów, to musimy wziąć
 do
do
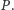 W ten sposób otrzymaliśmy następującą regułę
redukcyjną:
W ten sposób otrzymaliśmy następującą regułę
redukcyjną:
jeśli w grafie
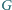 jest wierzchołek
jest wierzchołek
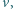 który ma co najmniej
który ma co najmniej
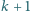 sąsiadów, wyrzuć z
sąsiadów, wyrzuć z
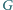 wierzchołek
wierzchołek
 oraz incydentne
z nim krawędzie oraz zmniejsz
oraz incydentne
z nim krawędzie oraz zmniejsz
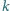 o jeden.
o jeden.
W wyniku zastosowania tej reguły otrzymaliśmy równorzędną instancję
problemu pokrycia wierzchołkowego: w zredukowanym grafie istnieje pokrycie
wierzchołkowe rozmiaru co najwyżej
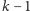 wtedy i tylko wtedy, gdy
w oryginalnym grafie istniało pokrycie wierzchołkowe rozmiaru co najwyżej
wtedy i tylko wtedy, gdy
w oryginalnym grafie istniało pokrycie wierzchołkowe rozmiaru co najwyżej
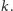
A co się dzieje, jeśli nie możemy zastosować powyższej reguły? Każdy
wierzchołek jest incydentny z co najwyżej
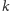 krawędziami, więc pokrycie
wierzchołkowe
krawędziami, więc pokrycie
wierzchołkowe
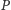 pokrywa co najwyżej
pokrywa co najwyżej
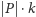 krawędzi. Czyli,
jeśli nie możemy zastosować naszej reguły, a zostało nam więcej niż
krawędzi. Czyli,
jeśli nie możemy zastosować naszej reguły, a zostało nam więcej niż
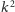 krawędzi, możemy śmiało odpowiedzieć „NIE”.
krawędzi, możemy śmiało odpowiedzieć „NIE”.
Otrzymaliśmy właśnie coś, co informatycy nazywają jądrem (ang. kernel)
problemu pokrycia wierzchołkowego: pokazaliśmy szybki algorytm, który albo
rozwiązuje problem pokrycia wierzchołkowego, albo znajduje równoważną
instancję problemu o co najwyżej
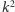 krawędziach. Zwróćmy uwagę na
to, że rozmiar zredukowanego grafu zależy tylko od parametru
krawędziach. Zwróćmy uwagę na
to, że rozmiar zredukowanego grafu zależy tylko od parametru
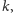 a nie od rozmiaru wyjściowego grafu: początkowy graf mógł być
olbrzymi.
a nie od rozmiaru wyjściowego grafu: początkowy graf mógł być
olbrzymi.
A może da się lepiej? Zredukowaliśmy graf do
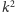 krawędzi, ale może
da się jeszcze ograniczyć liczbę wierzchołków? Zacznijmy od prostej
obserwacji: z grafu
krawędzi, ale może
da się jeszcze ograniczyć liczbę wierzchołków? Zacznijmy od prostej
obserwacji: z grafu
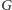 możemy wyrzucić wszystkie wierzchołki
izolowane. Zostanie nam co najwyżej
możemy wyrzucić wszystkie wierzchołki
izolowane. Zostanie nam co najwyżej
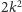 wierzchołków. Pokażemy
teraz inną regułę redukcyjną – istotnie bardziej skomplikowaną od poprzedniej –
która prowadzi do dużo mniejszego grafu: zredukujemy liczbę wierzchołków
do
wierzchołków. Pokażemy
teraz inną regułę redukcyjną – istotnie bardziej skomplikowaną od poprzedniej –
która prowadzi do dużo mniejszego grafu: zredukujemy liczbę wierzchołków
do
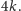 Załóżmy więc, że
Załóżmy więc, że
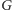 ma więcej niż
ma więcej niż
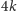 wierzchołków.
wierzchołków.
Aproksymując pokrycie wierzchołkowe, Marek Cygan używał skojarzeń. My
również ich użyjmy. Skojarzeniem w grafie nazywamy zbiór krawędzi,
w którym żadne dwie nie mają wspólnego końca. Istnieje szybki algorytm
znajdujący najliczniejsze skojarzenie w dowolnym grafie – załóżmy więc, że
znamy
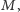 najliczniejsze skojarzenie w grafie
najliczniejsze skojarzenie w grafie
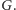 Zauważmy, iż
w dowolnym pokryciu wierzchołkowym musi być co najmniej jeden
koniec każdej krawędzi z
Zauważmy, iż
w dowolnym pokryciu wierzchołkowym musi być co najmniej jeden
koniec każdej krawędzi z
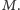 Skoro te nie są incydentne, to jeśli
Skoro te nie są incydentne, to jeśli
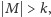 możemy od razu odpowiedzieć „NIE”. Załóżmy więc dalej,
że
możemy od razu odpowiedzieć „NIE”. Załóżmy więc dalej,
że
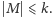
Niech
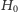 będzie zbiorem wierzchołków, które są końcami krawędzi
w
będzie zbiorem wierzchołków, które są końcami krawędzi
w
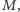 a
a
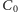 niech będzie zbiorem pozostałych wierzchołków. Skoro
niech będzie zbiorem pozostałych wierzchołków. Skoro
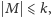 to
to
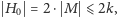 czyli
czyli
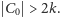 Co więcej,
zauważmy, że w
Co więcej,
zauważmy, że w
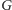 nie ma żadnej krawędzi łączącej dwa wierzchołki w
nie ma żadnej krawędzi łączącej dwa wierzchołki w
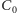 : gdyby była, moglibyśmy dodać ją do
: gdyby była, moglibyśmy dodać ją do
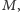 powiększając
liczność skojarzenia.
powiększając
liczność skojarzenia.
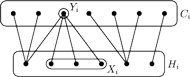
Rys. 1 Krok konstrukcyjny: wybór
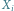 oraz
oraz
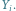
Uwaga, teraz będziemy robić coś skomplikowanego. Wyrzućmy z grafu
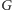 wszystkie krawędzie o obu końcach w
wszystkie krawędzie o obu końcach w
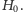 Otrzymamy
wówczas graf dwudzielny
Otrzymamy
wówczas graf dwudzielny
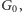 który z jednej strony będzie miał
który z jednej strony będzie miał
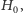 a z drugiej
a z drugiej
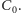 Sprawdźmy, czy w tym grafie istnieje
skojarzenie rozmiaru
Sprawdźmy, czy w tym grafie istnieje
skojarzenie rozmiaru
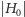 (czyli największe możliwe). Jeśli nie istnieje,
to, z twierdzenia Halla, istnieje zbiór
(czyli największe możliwe). Jeśli nie istnieje,
to, z twierdzenia Halla, istnieje zbiór
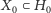 i zbiór jego sąsiadów
i zbiór jego sąsiadów
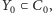 taki że
taki że
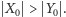 Wyrzućmy z grafu
Wyrzućmy z grafu
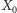 i
i
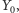 tj. weźmy
tj. weźmy
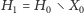 i
i
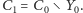 Postępujmy tak
do skutku, tj. mając dane
Postępujmy tak
do skutku, tj. mając dane
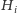 i
i
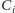 :
:
- 1.
- konstruujemy graf dwudzielny
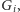 biorąc z grafu
biorąc z grafu
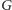 tylko
krawędzie łączące
tylko
krawędzie łączące
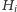 z
z
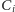 ;
;
- 2.
- sprawdzamy, czy istnieje w tym grafie skojarzenie rozmiaru
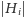 – jeśli tak, to koniec;
– jeśli tak, to koniec;
- 3.
- jeśli nie, to korzystając z twierdzenia Halla,
znajdujemy zbiór
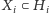 i zbiór jego sąsiadów
i zbiór jego sąsiadów
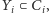 taki że
taki że
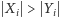 ;
;
- 4.
- przypisujemy
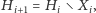
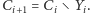
Pomińmy tutaj problem, jak znajdować zbiory
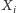 i
i
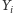 : wystarczy
nam informacja, że można to zrobić w czasie wielomianowym. Zauważmy,
że postępując według powyższej procedury, utrzymujemy następujące
niezmienniki:
: wystarczy
nam informacja, że można to zrobić w czasie wielomianowym. Zauważmy,
że postępując według powyższej procedury, utrzymujemy następujące
niezmienniki:
- 1.
- w
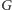 nie ma krawędzi łączącej dwa wierzchołki ze zbioru
nie ma krawędzi łączącej dwa wierzchołki ze zbioru
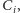 gdyż
gdyż
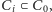 a ten warunek był spełniony już dla
a ten warunek był spełniony już dla
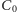 ;
;
- 2.
-
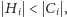 bo
bo
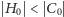 i w każdym kroku
i w każdym kroku
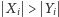 ;
;
- 3.
- zawsze
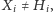 gdyż zbiorem sąsiadów
gdyż zbiorem sąsiadów
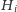 jest całe
jest całe
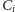 – żaden z wierzchołków
– żaden z wierzchołków
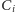 nie jest izolowany, bo te
usunęliśmy. A zatem
nie jest izolowany, bo te
usunęliśmy. A zatem
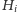 nigdy nie stanie się puste;
nigdy nie stanie się puste;
- 4.
-
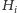 jest zbiorem sąsiadów
jest zbiorem sąsiadów
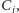 gdyż za każdym razem
usuwając z
gdyż za każdym razem
usuwając z
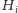 zbiór
zbiór
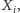 ze zbioru
ze zbioru
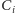 usuwamy
usuwamy
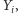 czyli wszystkich sąsiadów
czyli wszystkich sąsiadów
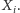
W związku z tym, gdy nasza procedura zakończy działanie, otrzymamy
niepuste zbiory wierzchołków
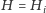 oraz
oraz
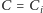 o następujących
własnościach:
o następujących
własnościach:
- 1.
- w
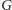 nie ma krawędzi łączącej dwa wierzchołki z
nie ma krawędzi łączącej dwa wierzchołki z
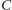 ;
;
- 2.
- istnieje skojarzenie
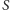 rozmiaru
rozmiaru
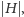 w którym każda
krawędź łączy wierzchołek z
w którym każda
krawędź łączy wierzchołek z
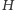 z wierzchołkiem z
z wierzchołkiem z
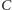 ;
;
- 3.
-
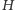 jest zbiorem sąsiadów
jest zbiorem sąsiadów
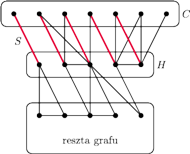
Rys. 2 Rozkład koronny grafu
To, co właśnie otrzymaliśmy, nazywamy rozkładem koronnym (ang. crown
decomposition) grafu: mamy koronę
 leżącą na głowie
leżącą na głowie
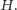 Zauważmy, że w dowolnym pokryciu wierzchołkowym w grafie
Zauważmy, że w dowolnym pokryciu wierzchołkowym w grafie
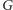 musimy wybrać co najmniej
musimy wybrać co najmniej
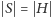 wierzchołków spośród
wierzchołków spośród
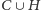 – musimy wybrać po końcu każdej krawędzi z
– musimy wybrać po końcu każdej krawędzi z
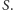 Ale,
z drugiej strony, biorąc do pokrycia wierzchołkowego całe
Ale,
z drugiej strony, biorąc do pokrycia wierzchołkowego całe
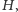 pokrywamy
wszystkie krawędzie incydentne z
pokrywamy
wszystkie krawędzie incydentne z
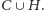 Możemy więc zachłannie
wziąć do pokrycia wierzchołkowego całe
Możemy więc zachłannie
wziąć do pokrycia wierzchołkowego całe
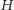 i usunąć z grafu
wierzchołki
i usunąć z grafu
wierzchołki
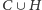 oraz incydentne z nimi krawędzie. Tym samym
zmniejszyliśmy rozmiar grafu.
oraz incydentne z nimi krawędzie. Tym samym
zmniejszyliśmy rozmiar grafu.
Zastanówmy się, co właśnie osiągnęliśmy. Wyszliśmy od takiej instancji
problemu pokrycia wierzchołkowego (grafu
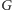 oraz parametru
oraz parametru
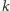 ),
że graf
),
że graf
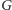 miał więcej niż
miał więcej niż
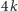 wierzchołków. Przeraźliwie
Uważny Czytelnik zauważy także, że w powyższej konstrukcji po kryjomu
założyliśmy
wierzchołków. Przeraźliwie
Uważny Czytelnik zauważy także, że w powyższej konstrukcji po kryjomu
założyliśmy
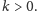 Możemy, dla danego grafu
Możemy, dla danego grafu
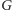 z parametrem
z parametrem
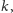 powtarzać powyższą redukcję, dopóki jest to możliwe. Zauważmy,
iż przy redukcji parametr
powtarzać powyższą redukcję, dopóki jest to możliwe. Zauważmy,
iż przy redukcji parametr
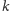 może się zmieniać – ale zawsze będzie
malał. Mamy trzy możliwe zakończenia tej procedury: Zastanówmy się,
co właśnie osiągnęliśmy. Wyszliśmy od takiej instancji problemu
pokrycia wierzchołkowego (grafu
może się zmieniać – ale zawsze będzie
malał. Mamy trzy możliwe zakończenia tej procedury: Zastanówmy się,
co właśnie osiągnęliśmy. Wyszliśmy od takiej instancji problemu
pokrycia wierzchołkowego (grafu
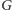 oraz parametru
oraz parametru
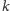 ), że
graf
), że
graf
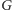 miał więcej niż
miał więcej niż
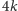 wierzchołków. Przeraźliwie
Uważny Czytelnik zauważy także, że w powyższej konstrukcji po
kryjomu założyliśmy
wierzchołków. Przeraźliwie
Uważny Czytelnik zauważy także, że w powyższej konstrukcji po
kryjomu założyliśmy
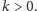 Możemy, dla danego grafu
Możemy, dla danego grafu
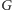 z parametrem
z parametrem
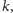 powtarzać powyższą redukcję, dopóki jest to
możliwe. Zauważmy, iż przy redukcji parametr
powtarzać powyższą redukcję, dopóki jest to
możliwe. Zauważmy, iż przy redukcji parametr
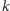 może się
zmieniać – ale zawsze będzie malał. Mamy trzy możliwe zakończenia tej
procedury:
może się
zmieniać – ale zawsze będzie malał. Mamy trzy możliwe zakończenia tej
procedury:
- 1.
- pewna redukcja odpowie „NIE”, gdyż rozmiar skojarzenia
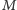 będzie za duży – wówczas wiemy, że w początkowym grafie
odpowiedź też była „NIE”;
będzie za duży – wówczas wiemy, że w początkowym grafie
odpowiedź też była „NIE”;
- 2.
- otrzymamy w wyniku
redukcji parametr
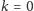 – wówczas odpowiedź brzmi „TAK”,
jeśli w grafie nie pozostała żadna krawędź, lub „NIE” w przeciwnym
przypadku;
– wówczas odpowiedź brzmi „TAK”,
jeśli w grafie nie pozostała żadna krawędź, lub „NIE” w przeciwnym
przypadku;
- 3.
- otrzymamy nowy
zredukowany graf
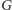 z nowym parametrem
z nowym parametrem
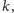 taki że graf
taki że graf
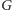 ma co najwyżej
ma co najwyżej
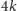 wierzchołków.
wierzchołków.
Pokazaliśmy właśnie, że algorytm polegający na aplikowaniu opisanej redukcji,
dopóki jest to możliwe, prowadzi do zredukowania wyjściowego grafu
do rozmiaru co najwyżej
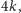 gdzie
gdzie
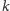 jest parametrem
zredukowanej instancji, a więc jest nie większy od parametru oryginalnej
instancji.
jest parametrem
zredukowanej instancji, a więc jest nie większy od parametru oryginalnej
instancji.
Wykonując powyższą konstrukcję trochę uważniej, można otrzymać jądro o
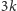 wierzchołkach, a komplikując dużo bardziej, da się dojść do
algorytmu redukującego graf do
wierzchołkach, a komplikując dużo bardziej, da się dojść do
algorytmu redukującego graf do
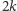 wierzchołków. Z drugiej strony,
ostatnio udowodniono, że przy pewnych, rozsądnych założeniach z teorii
złożoności nie istnieje jądro o
wierzchołków. Z drugiej strony,
ostatnio udowodniono, że przy pewnych, rozsądnych założeniach z teorii
złożoności nie istnieje jądro o
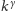 krawędziach dla żadnego
krawędziach dla żadnego
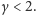
Wiele NP-trudnych problemów ma niewielkie jądra. Bardzo często algorytmy redukujące są proste, opierają się na kombinatorycznych spostrzeżeniach, a nie na wielkiej teorii. Można by całą Deltę wypełnić opisami algorytmów jak ten powyżej, ale może jednak tego nie róbmy.
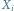 oraz
oraz