Drzewo Steinera: jedno zagadnienie, mnóstwo problemów
W naszym zespole badawczym analizujemy wiele różnych zagadnień, które występują w różnych aspektach. Nic w tym dziwnego, wszak algorytmika jest bardzo szeroką dziedziną. Zdarza się i tak, że to samo zagadnienie pojawia się w wielu kontekstach. Taka sytuacja ma miejsce w przypadku problemu drzewa Steinera.
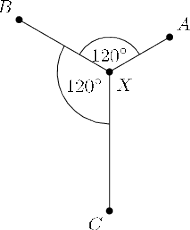
Rys. 1 Punkt
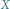 jest punktem Steinera dla wierzchołków
jest punktem Steinera dla wierzchołków
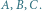
Zanim przejdziemy do formalnej definicji, przyjrzyjmy się nastepującemu
klasycznemu problemowi geometrycznemu. Książę Piotruś jest władcą trzech
miast:
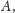
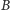 i
i
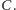 Chce je połączyć drogami tak, by
z każdego miasta dało się dojechać do każdego innego, i oczywiście pragnie
zminimalizować koszt budowy, czyli sumę długości zbudowanych dróg. Jedną
z dostępnych opcji jest zbudowanie dróg wzdłuż dwóch krótszych
boków trójkąta
Chce je połączyć drogami tak, by
z każdego miasta dało się dojechać do każdego innego, i oczywiście pragnie
zminimalizować koszt budowy, czyli sumę długości zbudowanych dróg. Jedną
z dostępnych opcji jest zbudowanie dróg wzdłuż dwóch krótszych
boków trójkąta
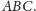 Jednak, co dla niektórych Czytelników
może być zaskakujące, można lepiej! O ile tylko każdy kąt wewnętrzny
trójkąta
Jednak, co dla niektórych Czytelników
może być zaskakujące, można lepiej! O ile tylko każdy kąt wewnętrzny
trójkąta
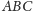 ma miarę mniejszą niż
ma miarę mniejszą niż
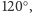 taniej jest zrobić
tak: znajdujemy wewnątrz trójkąta
taniej jest zrobić
tak: znajdujemy wewnątrz trójkąta
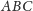 punkt
punkt
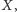 taki że
taki że
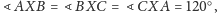 i budujemy drogi
i budujemy drogi
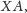
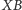 i
i
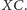 Czasem więc opłaca się wyjść poza schemat
prowadzenia dróg bezpośrednio między miastami i zbudować dodatkowe
skrzyżowanie. To dodatkowe skrzyżowanie nazywa się często punktem
Steinera.
Czasem więc opłaca się wyjść poza schemat
prowadzenia dróg bezpośrednio między miastami i zbudować dodatkowe
skrzyżowanie. To dodatkowe skrzyżowanie nazywa się często punktem
Steinera.
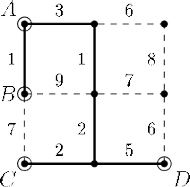
Rys. 2 Cztery zaznaczone wierzchołki to terminale. Pozostałe wierzchołki oraz krawędzie to możliwe skrzyżowania i drogi. Pogrubionymi kreskami zaznaczono krawędzie najtańszego drzewa Steinera, którego koszt to 14.
Przełóżmy teraz problem księcia Piotrusia na język teorii grafów. Mamy dany
spójny graf nieskierowany
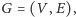 w którym każda krawędź
w którym każda krawędź
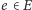 ma swoją długość
ma swoją długość
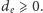 Graf to cały świat księcia
Piotrusia: wierzchołki grafu odpowiadają możliwym skrzyżowaniom,
a krawędzie możliwym drogom. Księstwo księcia Piotrusia to podzbiór
wierzchołków
Graf to cały świat księcia
Piotrusia: wierzchołki grafu odpowiadają możliwym skrzyżowaniom,
a krawędzie możliwym drogom. Księstwo księcia Piotrusia to podzbiór
wierzchołków
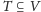 : te wierzchołki reprezentują miasta, które chcemy
połączyć drogami. Mamy znaleźć najtańszą sieć dróg – czyli spójny
podgraf grafu
: te wierzchołki reprezentują miasta, które chcemy
połączyć drogami. Mamy znaleźć najtańszą sieć dróg – czyli spójny
podgraf grafu
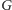 – która łączy wszystkie miasta – czyli wierzchołki zbioru
– która łączy wszystkie miasta – czyli wierzchołki zbioru
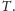 Zauważmy, że ten najtańszy podgraf zawsze będzie drzewem.
Zbiór
Zauważmy, że ten najtańszy podgraf zawsze będzie drzewem.
Zbiór
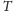 często nazywa się zbiorem terminali. Tak określone
zagadnienie to problem znalezienia najtańszego drzewa Steinera dla zbioru
terminali
często nazywa się zbiorem terminali. Tak określone
zagadnienie to problem znalezienia najtańszego drzewa Steinera dla zbioru
terminali
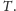 Przykładowy graf z czterema terminalami znajduje się na
rysunku 2.
Przykładowy graf z czterema terminalami znajduje się na
rysunku 2.
Będziemy też czasem mówili o problemie drzewa Steinera bez długości;
wtedy zakładamy, że każda krawędź grafu ma długość jeden. Zauważmy,
że odpowiada to znalezieniu jak najmniejszego zbioru wierzchołków
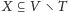 tak, by zbiór
tak, by zbiór
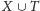 indukował spójny podgraf grafu
indukował spójny podgraf grafu
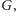 tzn. aby krawędzie, których oba końce znajdują się w tym zbiorze,
wystarczały do tego, aby z każdego terminalu dało się dojść do każdego
innego terminalu. Zbiór
tzn. aby krawędzie, których oba końce znajdują się w tym zbiorze,
wystarczały do tego, aby z każdego terminalu dało się dojść do każdego
innego terminalu. Zbiór
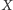 reprezentuje dodatkowe wierzchołki poza
reprezentuje dodatkowe wierzchołki poza
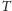 w poszukiwanym drzewie Steinera. Jeśli weźmiemy
w poszukiwanym drzewie Steinera. Jeśli weźmiemy
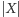 dodatkowych wierzchołków, to drzewo rozpinające
dodatkowych wierzchołków, to drzewo rozpinające
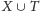 będzie miało
będzie miało
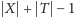 krawędzi i taki sam będzie koszt budowy dróg, co oznacza,
że minimalizując
krawędzi i taki sam będzie koszt budowy dróg, co oznacza,
że minimalizując
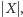 minimalizujemy sumę długości krawędzi
wybranych do drzewa Steinera.
minimalizujemy sumę długości krawędzi
wybranych do drzewa Steinera.
Problem drzewa Steinera, nawet w wersji bez długości, jest NP-trudny, co oznacza, że najprawdopodobniej nie da się efektywnie znajdować optymalnych rozwiązań tego zagadnienia. Wobec tego będziemy próbowali radzić sobie z nim w dwojaki sposób: dla większych instancji (tj. większych danych wejściowych problemu) wystarczy nam rozwiązanie przybliżone, natomiast rozwiązanie dokładne będziemy znajdować w czasie wykładniczym dla grafów na tyle dużych, na ile pozwoli nam złożoność naszego algorytmu oraz moc obliczeniowa komputera.
Zacznijmy od najbardziej klasycznej metody radzenia sobie z problemami NP-trudnymi, czyli od algorytmów aproksymacyjnych. Chcemy szybko – w czasie wielomianowym od rozmiaru grafu – znaleźć drzewo Steinera, które niekoniecznie będzie najlepsze, ale będzie niewiele gorsze od optymalnego.
Aby otrzymać prosty algorytm aproksymacyjny, wróćmy do oryginalnego
problemu księcia Piotrusia na płaszczyźnie. Wymyślenie, by dodać punkt
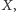 było dość trudne. A o ile gorzej byłoby, gdyby książę Piotruś
zbudował drogi wzdłuż dwóch krótszych boków trójkąta
było dość trudne. A o ile gorzej byłoby, gdyby książę Piotruś
zbudował drogi wzdłuż dwóch krótszych boków trójkąta
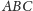 ?
Otóż okazuje się, że niewiele gorzej.
?
Otóż okazuje się, że niewiele gorzej.
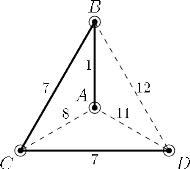
Rys. 3 Graf
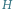 otrzymany poprzez wyznaczenie najkrótszych ścieżek pomiędzy każdą
parą terminali grafu z rysunku 2. Pogrubione krawędzie to minimalne drzewo rozpinające
otrzymany poprzez wyznaczenie najkrótszych ścieżek pomiędzy każdą
parą terminali grafu z rysunku 2. Pogrubione krawędzie to minimalne drzewo rozpinające
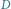 o koszcie 15.
o koszcie 15.
Przeanalizujmy ten pomysł w języku teorii grafów. Zmierzmy najkrótsze
odległości między każdą parą miast. Zbudujmy graf pełny
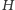 o zbiorze
wierzchołków
o zbiorze
wierzchołków
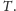 Dla miast
Dla miast
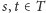 jako długość krawędzi
jako długość krawędzi
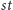 przyjmijmy długość najkrótszej ścieżki między
przyjmijmy długość najkrótszej ścieżki między
 i
i
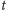 w grafie
w grafie
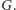 Graf
Graf
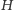 odpowiada grafowi składającemu się
z boków trójkąta
odpowiada grafowi składającemu się
z boków trójkąta
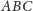 w rozpatrywanym na początku problemie na
płaszczyźnie, przy założeniu, że robotnicy księcia Piotrusia nie potrafią
budować dodatkowych skrzyżowań, ale potrafią budować najkrótsze drogi
między każdą parą miast. W grafie
w rozpatrywanym na początku problemie na
płaszczyźnie, przy założeniu, że robotnicy księcia Piotrusia nie potrafią
budować dodatkowych skrzyżowań, ale potrafią budować najkrótsze drogi
między każdą parą miast. W grafie
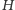 znajdźmy minimalne drzewo
rozpinające
znajdźmy minimalne drzewo
rozpinające
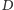 – można to zrobić wielomianowo za pomocą jednego
z klasycznych algorytmów, np. Kruskala lub Prima. Następnie dla każdej
krawędzi
– można to zrobić wielomianowo za pomocą jednego
z klasycznych algorytmów, np. Kruskala lub Prima. Następnie dla każdej
krawędzi
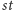 drzewa
drzewa
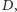 w grafie
w grafie
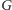 zbudujmy ciąg
dróg odpowiadający najkrótszej ścieżce między
zbudujmy ciąg
dróg odpowiadający najkrótszej ścieżce między
 i
i
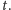 W
ten sposób w
W
ten sposób w
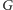 połączymy wszystkie miasta. Zauważmy, że
możliwa jest sytuacja, w której jedną drogę (krawędź oryginalnego
grafu) będziemy chcieli wybudować więcej niż raz, gdyż była ona
częścią kilku najkrótszych ścieżek wybranych do drzewa rozpinającego.
Jednakże w takim wypadku uzyskane drzewo Steinera będzie tańsze niż
drzewo
połączymy wszystkie miasta. Zauważmy, że
możliwa jest sytuacja, w której jedną drogę (krawędź oryginalnego
grafu) będziemy chcieli wybudować więcej niż raz, gdyż była ona
częścią kilku najkrótszych ścieżek wybranych do drzewa rozpinającego.
Jednakże w takim wypadku uzyskane drzewo Steinera będzie tańsze niż
drzewo
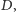 więc jest to dla nas sytuacja jak najbardziej korzystna.
Zastanówmy się, o ile droższe może być drzewo
więc jest to dla nas sytuacja jak najbardziej korzystna.
Zastanówmy się, o ile droższe może być drzewo
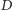 od rozwiązania
optymalnego?
od rozwiązania
optymalnego?
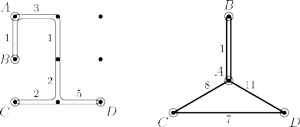
Rys. 4 Lewy rysunek przedstawia cykl Eulera otrzymany przez podwojenie krawędzi drzewa
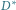 z rysunku 2. Po prawej stronie znajduje się zbiór krawędzi
z rysunku 2. Po prawej stronie znajduje się zbiór krawędzi
 rozpinający graf
rozpinający graf
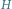 odpowiadający temu cyklowi Eulera (kolejne terminale na cyklu łączymy krawędziami w
odpowiadający temu cyklowi Eulera (kolejne terminale na cyklu łączymy krawędziami w
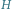 ).
).
Niech
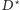 będzie optymalnym drzewem Steinera. Wykonujemy
następującą operację, kluczową dla całej analizy, mianowicie podwajamy
krawędzie drzewa
będzie optymalnym drzewem Steinera. Wykonujemy
następującą operację, kluczową dla całej analizy, mianowicie podwajamy
krawędzie drzewa
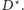 W ten sposób otrzymujemy graf spójny,
w którym każdy wierzchołek ma stopień parzysty. Ma on więc cykl
Eulera o długości równej dwukrotności kosztu drzewa
W ten sposób otrzymujemy graf spójny,
w którym każdy wierzchołek ma stopień parzysty. Ma on więc cykl
Eulera o długości równej dwukrotności kosztu drzewa
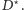 Zauważmy, że fragmenty cyklu prowadzące pomiędzy kolejnymi terminalami
mają długości co najmniej takie, jak długości odpowiednich krawędzi
w grafie
Zauważmy, że fragmenty cyklu prowadzące pomiędzy kolejnymi terminalami
mają długości co najmniej takie, jak długości odpowiednich krawędzi
w grafie
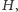 gdyż długości krawędzi w grafie
gdyż długości krawędzi w grafie
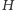 odpowiadają
najkrótszym ścieżkom w
odpowiadają
najkrótszym ścieżkom w
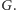 Zatem podwojony koszt drzewa
Zatem podwojony koszt drzewa
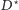 jest nie mniejszy niż koszt pewnego zbioru krawędzi
jest nie mniejszy niż koszt pewnego zbioru krawędzi
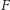 rozpinającego graf
rozpinającego graf
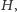 który to koszt jest z kolei nie mniejszy niż koszt
drzewa
który to koszt jest z kolei nie mniejszy niż koszt
drzewa
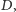 które jest minimalnym drzewem rozpinającym w grafie
które jest minimalnym drzewem rozpinającym w grafie
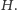 Stąd, nasz algorytm aproksymacyjny znajdzie drzewo Steinera
o koszcie nie większym niż dwukrotność kosztu optymalnego drzewa
Steinera.
Stąd, nasz algorytm aproksymacyjny znajdzie drzewo Steinera
o koszcie nie większym niż dwukrotność kosztu optymalnego drzewa
Steinera.
A czy da się lepiej? To znaczy, czy w czasie wielomianowym możliwe jest skonstruowanie drzewa Steinera, którego koszt będzie mniejszy niż dwukrotność optymalnego rozwiązania?
Okazuje się, że próbując lokalnie poprawiać otrzymane drzewo,
np. starając się wybierać wierzchołki Steinera o stopniu
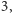 można
otrzymać trochę lepszy współczynnik aproksymacji (największy iloraz
znalezionego przez nas rozwiązania oraz rozwiązania optymalnego). Najlepszy
aktualnie znany algorytm aproksymacyjny dla problemu drzewa Steinera znajduje
zawsze rozwiązanie nie gorsze niż 1,39 optymalnego kosztu. Algorytm ten
pochodzi z 2010 roku, a jednym z jego autorów jest Jarosław Byrka
z Uniwersytetu Wrocławskiego.
można
otrzymać trochę lepszy współczynnik aproksymacji (największy iloraz
znalezionego przez nas rozwiązania oraz rozwiązania optymalnego). Najlepszy
aktualnie znany algorytm aproksymacyjny dla problemu drzewa Steinera znajduje
zawsze rozwiązanie nie gorsze niż 1,39 optymalnego kosztu. Algorytm ten
pochodzi z 2010 roku, a jednym z jego autorów jest Jarosław Byrka
z Uniwersytetu Wrocławskiego.
Na dziś starczy algorytmów aproksymacyjnych. Teraz będziemy próbowali rozwiązać problem drzewa Steinera w sposób dokładny, lecz w wersji bez długości. W tym sformułowaniu problem przejawia naturę kombinatoryczną.
Uporządkowanym etykietowanym drzewem nazwiemy drzewo
z wyróżnionym korzeniem, w którym zbiór synów każdego wierzchołka
jest uporządkowany (tzn. ich kolejność ma znaczenie). Każdy wierzchołek
takiego drzewa ma etykietę będącą identyfikatorem wierzchołka z grafu
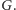 Aby uporządkowane etykietowane drzewo
Aby uporządkowane etykietowane drzewo
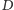 było poprawne, musi być
spełniony warunek, że jeśli w drzewie
było poprawne, musi być
spełniony warunek, że jeśli w drzewie
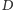 mamy krawędź łączącą
wierzchołki o etykietach
mamy krawędź łączącą
wierzchołki o etykietach
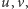 to w grafie
to w grafie
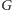 istnieje krawędź
istnieje krawędź
 Zauważmy, że nie wymagamy, aby etykiety wierzchołków drzewa
były różne, jednakże etykieta każdego wierzchołka jest różna od etykiety
ojca, gdyż w grafie
Zauważmy, że nie wymagamy, aby etykiety wierzchołków drzewa
były różne, jednakże etykieta każdego wierzchołka jest różna od etykiety
ojca, gdyż w grafie
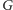 nie ma pętli.
nie ma pętli.
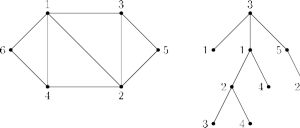
Rys. 5 Graf
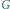 oraz jedno z poprawnych uporządkowanych etykietowanych drzew
oraz jedno z poprawnych uporządkowanych etykietowanych drzew
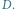 Zauważmy, że drzewo
Zauważmy, że drzewo
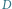 nie musi zawierać wszystkich etykiet wierzchołków z grafu
nie musi zawierać wszystkich etykiet wierzchołków z grafu
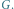
Zauważmy, że jeśli w grafie
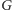 istnieje uporządkowane etykietowane
drzewo
istnieje uporządkowane etykietowane
drzewo
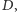 którego zbiór etykiet zawiera identyfikatory wszystkich
terminali, to optymalne drzewo Steinera ma nie więcej niż
którego zbiór etykiet zawiera identyfikatory wszystkich
terminali, to optymalne drzewo Steinera ma nie więcej niż
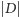 wierzchołków, gdyż możemy użyć drzewa
wierzchołków, gdyż możemy użyć drzewa
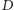 do konstrukcji zbioru
dróg, które rozpinają cały zbiór terminali.
do konstrukcji zbioru
dróg, które rozpinają cały zbiór terminali.
Wygodniej będzie, gdy zamienimy problem optymalizacyjny, jakim jest
poszukiwanie minimalnej liczby wierzchołków w drzewie Steinera, na problem
decyzyjny, w którym mamy stwierdzić, czy w danym grafie istnieje drzewo
Steinera zawierające nie więcej niż
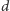 wierzchołków. Zamiast szukać
drzewa Steinera, będziemy szukać uporządkowanego etykietowanego drzewa
wierzchołków. Zamiast szukać
drzewa Steinera, będziemy szukać uporządkowanego etykietowanego drzewa
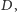 którego zbiór etykiet zawiera wszystkie identyfikatory terminali ze
zbioru
którego zbiór etykiet zawiera wszystkie identyfikatory terminali ze
zbioru
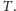 Okazuje się jednak, że dużo łatwiej szuka się drzewa, które
nie zawiera pewnych etykiet, dlatego też użyjemy zasady włączeń i wyłączeń
(czyli uogólnienia wzoru
Okazuje się jednak, że dużo łatwiej szuka się drzewa, które
nie zawiera pewnych etykiet, dlatego też użyjemy zasady włączeń i wyłączeń
(czyli uogólnienia wzoru
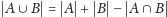 na większą liczbę
zbiorów). Niech
na większą liczbę
zbiorów). Niech
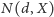 dla
dla
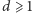 i
i
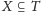 oznacza
liczbę uporządkowanych etykietowanych drzew o
oznacza
liczbę uporządkowanych etykietowanych drzew o
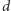 wierzchołkach,
których zbiór etykiet nie zawiera identyfikatorów terminali ze zbioru
wierzchołkach,
których zbiór etykiet nie zawiera identyfikatorów terminali ze zbioru
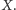 Wartość
Wartość
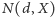 dla ustalonych
dla ustalonych
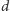 oraz
oraz
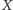 można obliczyć w czasie wielomianowym standardowym algorytmem
programowania dynamicznego, co pozostawiamy Drogiemu Czytelnikowi jako
ćwiczenie. Zauważmy też, że na mocy zasady włączeń i wyłączeń liczba
uporządkowanych drzew
można obliczyć w czasie wielomianowym standardowym algorytmem
programowania dynamicznego, co pozostawiamy Drogiemu Czytelnikowi jako
ćwiczenie. Zauważmy też, że na mocy zasady włączeń i wyłączeń liczba
uporządkowanych drzew
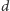 -wierzchołkowych zawierających wszystkie
etykiety ze zbioru
-wierzchołkowych zawierających wszystkie
etykiety ze zbioru
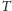 jest równa:
jest równa:

Skoro każdą wartość
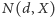 potrafimy obliczyć w czasie
wielomianowym, to powyższą sumę możemy obliczyć w czasie
potrafimy obliczyć w czasie
wielomianowym, to powyższą sumę możemy obliczyć w czasie
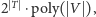 przy czym przez
przy czym przez
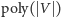 oznaczamy czas
wielomianowy względem
oznaczamy czas
wielomianowy względem
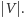 Ten algorytm zaprezentował w 2009 roku
Jesper Nederlof, a główną zaletą tej metody jest to, że zależność wykładnicza
dotyczy jedynie
Ten algorytm zaprezentował w 2009 roku
Jesper Nederlof, a główną zaletą tej metody jest to, że zależność wykładnicza
dotyczy jedynie
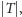 a nie całego
a nie całego
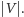 Pytaniem otwartym jest, czy
da się to zrobić szybciej, np. w czasie
Pytaniem otwartym jest, czy
da się to zrobić szybciej, np. w czasie
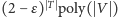 dla jakiegoś
dla jakiegoś
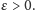
W artykule Pokrycie wierzchołkowe kontratakuje (Delta 4/2010) przedstawiliśmy
ideę kernelizacji. Algorytm kernelizacyjny to taki, który szybko (w czasie
wielomianowym) istotnie zmniejsza rozmiar problemu w ten sposób, że dla
zmniejszonej instancji wynik jest taki sam jak dla oryginalnej. Spróbujmy
zrozumieć, czego oczekiwalibyśmy od algorytmu kernelizacyjnego dla
problemu drzewa Steinera. Wejściem (decyzyjnej wersji) problemu drzewa
Steinera bez długości jest graf
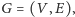 zbiór terminali (miast)
zbiór terminali (miast)
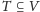 oraz liczba całkowita
oraz liczba całkowita
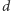 ; chcemy znaleźć drzewo
; chcemy znaleźć drzewo
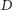 o co najwyżej
o co najwyżej
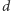 wierzchołkach, zawierające wszystkie
terminale. Chcielibyśmy w czasie wielomianowym zredukować rozmiar
grafu; powiedzmy, że oczekujemy, że po redukcji graf będzie wielkości
wielomianowej względem
wierzchołkach, zawierające wszystkie
terminale. Chcielibyśmy w czasie wielomianowym zredukować rozmiar
grafu; powiedzmy, że oczekujemy, że po redukcji graf będzie wielkości
wielomianowej względem
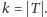 Pokażemy, dlaczego jest to
niemożliwe (przy odpowiednich założeniach teoriozłożonościowych).
Pokażemy, dlaczego jest to
niemożliwe (przy odpowiednich założeniach teoriozłożonościowych).
Na chwilę przenieśmy się do innego zagadnienia. W problemie znajdowania
motywu w grafie mamy dany graf
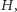 w którym każdy wierzchołek jest
pomalowany na jeden z
w którym każdy wierzchołek jest
pomalowany na jeden z
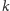 kolorów. Chcemy wybrać po jednym
wierzchołku każdego koloru tak, by wybrane wierzchołki tworzyły (indukowały)
graf spójny. Taki zbiór wierzchołków nazywamy motywem. Co może
wydać się zaskakujące, problem ten jest NP-trudny, nawet gdy
kolorów. Chcemy wybrać po jednym
wierzchołku każdego koloru tak, by wybrane wierzchołki tworzyły (indukowały)
graf spójny. Taki zbiór wierzchołków nazywamy motywem. Co może
wydać się zaskakujące, problem ten jest NP-trudny, nawet gdy
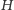 jest
drzewem, którego wszystkie wierzchołki mają stopień nie większy niż
trzy.
jest
drzewem, którego wszystkie wierzchołki mają stopień nie większy niż
trzy.
Zauważmy, że problem drzewa Steinera jest co najmniej tak trudny jak
problem znajdowania motywu w grafie. Faktycznie, istnieje sprowadzenie
(redukcja) przekształcające instancje problemu znajdowania motywu w grafie na
instancje problemu drzewa Steinera. Mając daną instancję problemu znajdowania
motywu w grafie
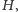 dla każdego koloru
dla każdego koloru
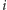 dodajemy terminal
dodajemy terminal
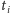 połączony ze wszystkimi wierzchołkami koloru
połączony ze wszystkimi wierzchołkami koloru
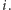 Łatwo
zauważyć, że drzewo Steinera o
Łatwo
zauważyć, że drzewo Steinera o
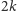 wierzchołkach w grafie
wierzchołkach w grafie
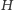 z dodanymi terminalami odpowiada motywowi w oryginalnym grafie
z dodanymi terminalami odpowiada motywowi w oryginalnym grafie
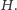 Jest tak dlatego, że dwa różne terminale nigdy nie mają
wspólnego sąsiada, co oznacza, że do drzewa Steinera musimy wybrać co
najmniej
Jest tak dlatego, że dwa różne terminale nigdy nie mają
wspólnego sąsiada, co oznacza, że do drzewa Steinera musimy wybrać co
najmniej
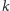 wierzchołków niebędących terminalami. Jednakże
szukamy drzewa o co najwyżej
wierzchołków niebędących terminalami. Jednakże
szukamy drzewa o co najwyżej
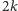 wierzchołkach, co oznacza, że
zbiór nieterminali, które wybierzemy do drzewa Steinera, musi być
spójny, gdyż nie możemy sobie pozwolić na wybranie żadnego
dodatkowego wierzchołka. Ten spójny zbiór nieterminali odpowiada
motywowi w oryginalnym grafie, jako że sąsiedzi różnych terminali mają
różne kolory.
wierzchołkach, co oznacza, że
zbiór nieterminali, które wybierzemy do drzewa Steinera, musi być
spójny, gdyż nie możemy sobie pozwolić na wybranie żadnego
dodatkowego wierzchołka. Ten spójny zbiór nieterminali odpowiada
motywowi w oryginalnym grafie, jako że sąsiedzi różnych terminali mają
różne kolory.
Teraz załóżmy, że mamy algorytm kernelizacyjny dla problemu drzewa
Steinera w grafie bez długości, tj. algorytm, który w czasie wielomianowym
redukuje rozmiar grafu
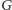 do wielkości wielomianowej od
do wielkości wielomianowej od
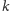 –
liczby terminali w grafie. Możemy wtedy wykonać następującą operację:
–
liczby terminali w grafie. Możemy wtedy wykonać następującą operację:
- 1.
- Załóżmy, że mamy dany długi ciąg instancji problemu znajdowania
motywu w grafie
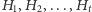 ; każda instancja ma dokładnie
; każda instancja ma dokładnie
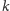 kolorów.
kolorów.
- 2.
- Tworzymy graf
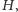 który jest sumą rozłączną wszystkich grafów
który jest sumą rozłączną wszystkich grafów
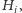
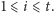 Kolory wierzchołków są takie same jak
w grafach
Kolory wierzchołków są takie same jak
w grafach
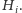 Zauważmy, że w grafie
Zauważmy, że w grafie
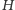 istnieje motyw
wtedy i tylko wtedy, gdy istnieje on w co najmniej jednym z grafów
istnieje motyw
wtedy i tylko wtedy, gdy istnieje on w co najmniej jednym z grafów
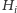 : motyw musi być spójny, więc musi zawierać się w jednej
spójnej składowej grafu
: motyw musi być spójny, więc musi zawierać się w jednej
spójnej składowej grafu
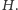
- 3.
- Redukujemy problem znajdowania
motywu w grafie
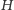 do problemu znajdowania drzewa Steinera, tak
jak w poprzednim akapicie: dodajemy po jednym terminalu każdego
koloru. Otrzymujemy graf
do problemu znajdowania drzewa Steinera, tak
jak w poprzednim akapicie: dodajemy po jednym terminalu każdego
koloru. Otrzymujemy graf
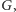 w którym szukamy drzewa Steinera
o
w którym szukamy drzewa Steinera
o
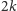 wierzchołkach.
wierzchołkach.
- 4.
- Na
grafie
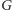 uruchamiamy algorytm kernelizacyjny, który zmniejsza
graf
uruchamiamy algorytm kernelizacyjny, który zmniejsza
graf
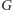 do rozmiarów wielomianowych względem
do rozmiarów wielomianowych względem
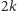 (czyli
wielomianowych względem
(czyli
wielomianowych względem
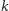 ).
).
Przeanalizujmy, co się stało. Liczba początkowych instancji –
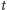 – mogła być
bardzo duża, ponadwielomianowa w stosunku do
– mogła być
bardzo duża, ponadwielomianowa w stosunku do
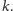 Na końcu
otrzymaliśmy jedną instancję problemu znajdowania drzewa Steinera o dużo
mniejszej liczbie wierzchołków – wielomianowej względem
Na końcu
otrzymaliśmy jedną instancję problemu znajdowania drzewa Steinera o dużo
mniejszej liczbie wierzchołków – wielomianowej względem
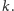 Przy tym ta
końcowa instancja jest „syntezą” początkowych instancji: istnieje w niej
odpowiednio małe drzewo Steinera wtedy i tylko wtedy, gdy co najmniej jedna
początkowa instancja miała motyw. Końcowa instancja jest jednak bardzo mała
i nie ma szans pomieścić informacji o wszystkich początkowych instancjach
problemu znajdowania motywu w grafie – intuicyjnie oznacza to, że
musieliśmy większość instancji
Przy tym ta
końcowa instancja jest „syntezą” początkowych instancji: istnieje w niej
odpowiednio małe drzewo Steinera wtedy i tylko wtedy, gdy co najmniej jedna
początkowa instancja miała motyw. Końcowa instancja jest jednak bardzo mała
i nie ma szans pomieścić informacji o wszystkich początkowych instancjach
problemu znajdowania motywu w grafie – intuicyjnie oznacza to, że
musieliśmy większość instancji
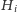 w jakiś sposób rozwiązać.
Okazuje się, że dla problemu NP-zupełnego taka operacja nie może nam się
udać; powyższe rozumowanie można sformalizować i pokazać, że
algorytm kernelizacyjny dla problemu drzewa Steinera pociągałby za sobą dużą
rewolucję w teorii złożoności, co jest mało prawdopodobne. Dodajmy tylko,
że użyta tutaj technika jest również stosunkowo nowa – pierwsi
użyli jej Lance Fortnow i Rahul Santhanam w swojej pracy z 2008
roku.
w jakiś sposób rozwiązać.
Okazuje się, że dla problemu NP-zupełnego taka operacja nie może nam się
udać; powyższe rozumowanie można sformalizować i pokazać, że
algorytm kernelizacyjny dla problemu drzewa Steinera pociągałby za sobą dużą
rewolucję w teorii złożoności, co jest mało prawdopodobne. Dodajmy tylko,
że użyta tutaj technika jest również stosunkowo nowa – pierwsi
użyli jej Lance Fortnow i Rahul Santhanam w swojej pracy z 2008
roku.
Jak widać, problem drzewa Steinera ma wiele ciekawych obliczy i każdy znajdzie w nim coś dla siebie. Barwne jest życie algorytmika.
Do grupy naukowej badającej różne aspekty problemów NP-trudnych na wydziale Matematyki, Informatyki i Mechaniki Uniwersytetu Warszawskiego należą dr Łukasz Kowalik, dr Marcin Mucha, dr hab. Piotr Sankowski, dr Jakub Wojtaszczyk, a także doktoranci i studenci wydziału, w tym autorzy tego artykułu. Główne kierunki badań stanowią aproksymacja oraz algorytmy dokładne dla problemów NP-trudnych. Prace, których autorami są członkowie zespołu, są publikowane na najlepszych międzynarodowych konferencjach poświęconych informatyce teoretycznej oraz w uznanych periodykach naukowych. Członkowie grupy są laureatami programów stypendialnych Fundacji Nauki Polskiej, miesięcznika Polityka i nagród im. Witolda Lipskiego. Ponadto prace naukowe grupy badawczej prowadzone są w ramach grantów MNiSW, jak również prestiżowego grantu „Starting Independent Researcher Grant” ufundowanego przez European Research Council, którego kierownikiem jest dr hab. Piotr Sankowski.
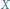 jest punktem Steinera dla wierzchołków
jest punktem Steinera dla wierzchołków
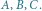
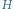 otrzymany poprzez wyznaczenie najkrótszych ścieżek pomiędzy każdą
parą terminali grafu z rysunku 2. Pogrubione krawędzie to minimalne drzewo rozpinające
otrzymany poprzez wyznaczenie najkrótszych ścieżek pomiędzy każdą
parą terminali grafu z rysunku 2. Pogrubione krawędzie to minimalne drzewo rozpinające
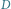 o koszcie 15.
o koszcie 15.
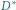 z rysunku 2. Po prawej stronie znajduje się zbiór krawędzi
z rysunku 2. Po prawej stronie znajduje się zbiór krawędzi
 rozpinający graf
rozpinający graf
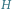 odpowiadający temu cyklowi Eulera (kolejne terminale na cyklu łączymy krawędziami w
odpowiadający temu cyklowi Eulera (kolejne terminale na cyklu łączymy krawędziami w
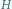 ).
).
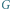 oraz jedno z poprawnych uporządkowanych etykietowanych drzew
oraz jedno z poprawnych uporządkowanych etykietowanych drzew
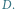 Zauważmy, że drzewo
Zauważmy, że drzewo
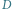 nie musi zawierać wszystkich etykiet wierzchołków z grafu
nie musi zawierać wszystkich etykiet wierzchołków z grafu