Formalna definicja funkcji, doskonale znana studentom I roku matematyki, opiera się na teorii mnogości. Funkcja jest po prostu dość specyficznym rodzajem zbioru, a mianowicie relacją (czyli pewnym zbiorem par uporządkowanych) lewostronnie całkowitą i prawostronnie jednoznaczną. Pozwolimy sobie pominąć definicje, które czytelnikom Delty mogą być znane, a nam są zbędne.

Oczywiście, jak to zwykle bywa, definicje swoje, a życie swoje. Gdy podsłuchamy rozmowy matematyków, okaże się, że funkcja to dla nich nie specjalnie spreparowany zbiór odpowiednich par, ale prawie żywa istota, która może wykonywać różne czynności. Oto jedna funkcja rośnie, gdy inna maleje. Niektóre funkcje osiągają swoje kresy, inne zaś uciekają do nieskończoności. Mało tego, zdarza się nawet, że funkcja znika w jakimś punkcie! Sposobów myślenia o funkcjach jest wiele. My skupimy się na jednym z nich, który jest chyba najbliższy praktyce programistycznej (co nie znaczy, że z nią tożsamy). Otóż funkcję możemy rozumieć jako model czynności obliczania czegoś - mówiąc językiem szkolnym, jako "wzór".

Z takim rozumieniem funkcji matematycy mają jednak kłopoty. Po pierwsze, nie każdą funkcję można opisać wzorem. Jest tak choćby dlatego, że "wzorów" jest przeliczalnie wiele, a rodziny funkcji o dziedzinach i przeciwdziedzinach nieskończonych są nieprzeliczalne. Gdybyśmy nawet ograniczyli rozważania tylko do funkcji dających się opisać wzorem (czego matematycy z różnych powodów nie chcą robić), nie rozwiąże to wszystkich problemów. Świetnie to widać na przykładzie porównywania funkcji. Zapytajmy w szczególności, czy funkcje o wzorach 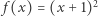i 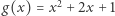są równe, innymi słowy, czy symbole 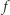i 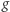oznaczają tę samą funkcję. Matematyk powie oczywiście, że tak - ale przecież te wzory nie są identyczne! Co gorsza, nierzadko zdarza się, że jest bardzo trudno orzec, czy dwa (różnie wyglądające) wzory opisują tę samą funkcję. Formalnie, jest to problem nierozstrzygalny. Intuicję tego pojęcia ma każdy, kto kiedykolwiek musiał dowodzić bardziej złożonych tożsamości trygonometrycznych lub wyliczać trudniejsze całki.

Coś, co dla matematyków jest kłopotliwe, dla programistów jest za to całkiem naturalne. Ponieważ program komputerowy to właśnie sformalizowany opis obliczania czegoś, koncepcja funkcji (czy wzoru) prawdopodobnie znakomicie nadaje się do opisu programów, prawda? Istotnie, większość języków programowania posiada funkcje, które - przynajmniej na pierwszy rzut oka - bardzo przypominają te znane z matematyki.W niektórych językach, na przykład w C, wykonanie programu oznacza właśnie wykonanie pewnej specjalnej funkcji "głównej". Przyjmują jakieś argumenty, zwracają jakieś wartości, często mają swoje specjalne nazwy... Może więc jednak (wbrew obiegowej opinii studentów informatyki) faktycznie programowanie to po prostu kawałek matematyki?

Cóż, okazuje się jednak, że sprawy nie wyglądają tak prosto. Podstawowym problemem jest to, że obiekty matematyczne są niezmienne w czasie. Jeżeli funkcji o wzorze 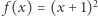damy liczbę 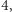to odda nam liczbę 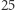- tak samo dzisiaj, jak i jutro czy za sto lat. Programy komputerowe (jak wszyscy pewnie tego doświadczyliśmy) potrafią się niekiedy zachować całkiem inaczej, mimo że użytkownik wykonuje dokładnie te same czynności!

Dlaczego tak jest? Jednym z powodów jest fakt, że - mimo tak samo brzmiącej nazwy - funkcja programisty jest jednak (mimo niewątpliwego podobieństwa) czymś innym niż funkcja matematyka.

Na czym polega różnica? Zamiast podawać formalne definicje, spójrzmy na przykłady.Nasze funkcje zapiszemy w języku Lua, który - z uwagi na swoją prostotę - świetnie nadaje się do naszych rozważań. Na początek coś, co bardzo przypomina funkcje znane z matematyki.

Powyższy zapis oznacza, że symbol f będzie nazwą funkcji jednoargumentowej, która dla argumentu x zwraca wartość wyrażenia (x+1)^2 - jest to więc odpowiednik funkcji 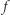z naszych poprzednich rozważań. Na razie jest dobrze, funkcja w programie dokładnie odpowiada funkcji w matematyce.

Skomplikujmy nieco sprawy i rozważmy taką funkcję:

Jak nietrudno zgadnąć, dla argumentu x wynoszącego na przykład 1 powyższa funkcja zwróci wartość (mniej więcej) 4.14159. Zauważmy, że nadal mamy matematyczny odpowiednik funkcji h, czyli funkcję daną wzorem 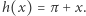Jest jednak pewien haczyk. Prawie jak w znanym dowcipie o liczbie 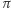i pociągu… Jak wiemy, 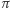jest znaną stałą matematyczną i zmienna math.pi w Lua ma wartość równą w przybliżeniu 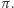Jest jednak ona tym, czym jest - zmienną właśnie (język Lua, w odróżnieniu od na przykład C, nie ma pojęcia stałej). Nic nie stoi więc na przeszkodzie, aby przed wywołaniem funkcji h (czyli nakazaniem komputerowi jej wykonania) napisać na przykład math.pi = 22/7. Formalnie, jest to instrukcja przypisania wartości 22/7 zmiennej math.pi. Wówczas okaże się, że wywołanie h(1) da wynik (mniej więcej) 4.142857.

Zatrzymajmy się na chwilę, żeby zrozumieć, co się stało. Dwukrotne wywołanie tej samej funkcji z tym samym argumentem dało różne wyniki! To nie do pomyślenia w matematyce. Dowcipnisie mogą argumentować, że w czasach Archimedesa faktycznie 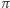wynosiło 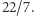W naszym programie wydarzyło się to z tego powodu, że funkcja h w trakcie swoich obliczeń bierze pod uwagę nie tylko wartości argumentów, ale również stan całego systemu (który może być różny w różnych chwilach). W przypadku funkcji h kluczowym elementem tego stanu jest wartość zmiennej math.pi. Inni dowcipnisie mogą powiedzieć, że jak to, wystarczy dodać zmienną pi jako dodatkowy parametr funkcji i problem znika. Teoretycznie tak, ale w praktyce jest z tym sporo problemów. W szczególności takie używanie funkcji byłoby skrajnie niewygodne, w bardziej skomplikowanych sytuacjach musiałyby one mieć po kilkanaście argumentów.

Gdy się nad tym zastanowić, komputer obliczający jedynie funkcje "matematyczne" byłby całkiem bezużyteczny - wykonanie każdego programu za każdym razem dawałoby identyczny wynik. My zaś potrzebujemy właśnie programów, które dają różne wyniki w zależności od sytuacji - chcemy oglądać różne strony internetowe, drukować różne dokumenty i wyliczać różne rzeczy. Dlatego wszystkie użyteczne programy biorą pod uwagę stan systemu (mogą to być dane wprowadzone przez użytkownika, zawartość dysku komputera w czasie działania programu, informacje dostępne "w internecie", czyli na innych komputerach, czy na przykład data i godzina uruchomienia programu). Co więcej, bardzo wiele programów ten stan zmienia - zapisuje coś w pamięci lub na dysku, albo wysyła "do internetu". O funkcjach, które zmieniają stan, mówi się, że mają efekty uboczne. Nazwa ta może być myląca, bo niektóre funkcje wywołuje się wyłącznie po to, aby zmienić stan!

Czy to źle? Zależy, jak patrzeć. Jak właśnie zobaczyliśmy, odczytywanie i zmiana stanu wydaje się konieczna, aby programy mogły być użyteczne. Musimy za to jednak zapłacić pewną cenę. Funkcje czyste (bo tak programiści nazywają funkcje, które ani nie korzystają ze stanu, ani go nie zmieniają) są czasami łatwiejsze do napisania, zwykle o wiele łatwiejsze do przetestowania, a przede wszystkim pozwalają uniknąć niektórych pomyłek. Programiści nauczyli się przez ostatnie kilkadziesiąt lat, że wszystko, co ułatwia ich pracę i pomaga popełnić mniej błędów, jest na wagę złota. Stopień skomplikowania współczesnych systemów informatycznych jest tak duży, że znacząca część pracy nad nimi to szukanie i naprawienie usterek, które prędzej czy później (a raczej prędzej) się pojawią. Jednym ze sposobów jest właśnie takie zaprojektowanie systemu, żeby jak największa jego część składała się z funkcji czystych, a konieczne operacje na stanie były wyizolowane w osobnej, niewielkiej jego części. W ostatnich latach taka metoda, zwana programowaniem funkcyjnym, zrobiła się modna w świecie programistycznym, a narzędzia pozwalające na jej stosowanie pojawiły się w bardzo wielu językach programowania. Koniec końców okazuje się, że idee matematyczne jednak potrafią się przydać do czegoś pożytecznego...