Buntownicy, jak zawsze, idą w drugą stronę. Od roku 1984 organizowany jest konkurs International Obfuscated C Code Contest na napisanie możliwie nieczytelnego programu w języku C. Poniżej umieściliśmy zgłoszenie Nicolasa Ollingera, które w roku 2001 (ex aequo z Jasonem Orendorffem) zdobyło główną nagrodę. Czytelnik Chorobliwie Zawzięty może sprawdzić, że ten program realizuje działanie sita Eratostenesa.

Problem zaciemniania programów jednak wybiega daleko poza obszar sztubackich żartów.

Zaciemnianie (fachowo: obfuskacja) kodu źródłowego programu to jedno z ważnych wyzwań kryptologii. Motywacja do badania tego problemu jest chyba dość jasna. Dla zapewnienia bezpieczeństwa danych (albo z powodów czysto biznesowych) czasem autor programu chce tylko umożliwić jego wykonywanie komuś innemu, ale wcale nie chce ujawniać szczegółów jego działania. W dobie Internetu takie założenie trywialnie można zrealizować w modelu klient-serwer. 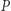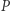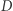Wystarczy założyć, że kod pewnego programu znany jest tylko serwerowi, a jeśli użytkownik chce wykonać na danych to powinien wysłać do serwera, a ten obliczy i odeśle mu 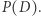Problem obfuskacji jest jednak trudniejszy. Chcemy mieć własność jak wyżej, ale w świecie off-line. Innymi słowy: zakładamy, że użytkownik przechowuje sam kod programu 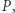a i tak najlepsze, co może zrobić, by poznać jego działanie, to uruchamiać 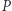na różnych danych i odczytywać wyniki. Chcielibyśmy, aby kod był tak zagmatwany, żeby każda próba jego obejrzenia i wyciągnięcia jakichś bardziej ogólnych wniosków musiała kończyć się niepowodzeniem.

Jak w całej kryptologii, początkowo do problemu zaciemniania kodu podchodzono w sposób nieformalny (czy raczej: niematematyczny). To znaczy definicje problemu były nieostre, a rozwiązania dyskutowane były wyłącznie na poziomie intuicyjno-inżynierskim. Sprawę zmieniła słynna prorocza praca New Directions in Cryptography Diffiego i Hellmana z roku 1976, w której (między innymi) podjęto próbę sformalizowania pojęcia obfuskacji programu. Konkretnie: niech 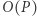oznacza próbę zaciemnienia programu 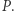Powiemy, że 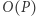jest rzeczywiście obfuskacją 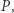gdy (1) dla każdego wejścia, 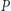oraz 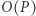dają ten sam wynik oraz (2) dla każdego (wielomianowego) użytkownika 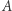istnieje taki symulator 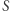(czyli po prostu pewien wielomianowy program), że:

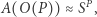
gdzie: 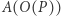oznacza wynik działania 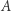na danym kodzie 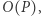a 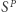oznacza wynik działania 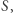który ma dostęp do serwera takiego, jak w akapicie wyżej (czyli obliczającego na żądanie wartości programu 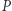). Wyniki programów nie muszą być deterministyczne, stąd znaczek " " oznacza tutaj bliskość rozkładów możliwych wyników. Intuicyjnie ta definicja głosi, że użytkownik 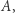który ma pełny dostęp do kodu 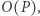nie ma specjalnej przewagi nad użytkownikiem dysponującym tylko dostępem do serwera, skoro ten drugi może symulować (w czasie wielomianowym i z dużą dokładnością) wynik obliczeń tego pierwszego.

Marzeniem kryptologów przez wiele lat pozostawał uniwersalny kompilator, który dla każdego programu potrafiłby wyznaczyć jego nową wersję, zaciemnioną według definicji wyżej. Niestety, w roku 2001 Barak et al. udowodnili, że taka uniwersalna konstrukcja nie może istnieć. Na długi czas ostudziło to zapał środowiska. Jednak przełom pojawił się w roku 2013, gdy kolejna grupa badaczy, pracując ze słabszą wersją definicji obfuskacji (indistinguishability obfuscation, w skrócie iO), wskazała (bez dowodu) obiecującego kandydata na uniwersalny kompilator. Od tamtej pory ruszyła lawina. Znamy już wiele uniwersalnych kompilatorów iO, dowodliwie poprawnych przy różnych, mniej lub bardziej egzotycznych założeniach. Znamy też wiele zastosowań, pokazujących, że sama definicja (nieprezentowana w tym tekście) iO nie jest za słaba w praktyce. Wciąż jednak wiele bardzo ważnych pytań w tej dziedzinie pozostaje bez odpowiedzi. Przede wszystkim: