Dziś powszechnie stosowany i uznawany jest pomysł, żeby szybkość algorytmu mierzyć liczbą operacji przez niego wykonywaną w zależności od wielkości wejścia. Za rozsądnie szybkie uznaje się algorytmy, które dla wejścia rozmiaru 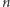zwracają odpowiedź po wykonaniu co najwyżej 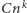operacji dla pewnych 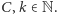Mówimy wówczas, że działają w czasie 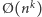i nazywamy je algorytmami wielomianowymi. Co prawda, w pewnych dziedzinach nie jest to założenie powszechne. Na przykład w dziedzinie baz danych, gdzie rozmiar wejścia bywa wielkości miliardów lub bilionów, za wolne są już w zasadzie nawet algorytmy kwadratowe. Ale jednak klasycznie uznaje się algorytmy wielomianowe za rozsądnie szybkie - zwykle, gdy istnieje jakiś algorytm wielomianowy, to istnieje również algorytm wielomianowy o niewielkim wykładniku. I wszystko byłoby dobrze, gdyby nie to, że złożoność pesymistyczna tak naprawdę nie do końca odpowiada temu, czego potrzebujemy w praktyce.

Najbardziej chyba znanym przykładem tej niezgodności jest algorytm quicksort. Wiele algorytmów sortujących działa w pesymistycznym czasie 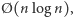quicksort natomiast w 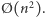Jednak okazuje się, że w praktyce zwykle działa dosyć szybko, zupełnie nie zbliżając się do 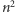operacji. Wypadałoby uzasadnić, co takiego w sobie ma quicksort, że w praktyce działa szybko. W związku z tym wprowadzono pojęcie średniej złożoności czasowej. Po prostu zamiast najdłuższego czasu działania dla wejścia rozmiaru bierzemy średnią ze wszystkich czasów działania dla wejść rozmiaru 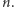Przykładowo dla quicksortu bierzemy każdą z 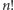permutacji 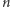elementów z prawdopodobieństwem 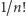i obliczamy średnią. Wychodzi rzeczywiście wynik rzędu 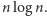Złożoność średnia stała się bardzo popularna do badania "bardziej praktycznej" złożoności czasowej programów. Jednak i ona ma swoje wady.

Mianowicie, założenie, że każde możliwe wejście jest równo prawdopodobne, jest nie zawsze prawdziwe. Akurat dla sortowania jest to często założenie w miarę rozsądne, bo wydaje się, że każda kolejność elementów na wejściu jest mniej więcej równo prawdopodobna. Jednak wyobraźmy sobie, że rozważamy graf ważony opisujący połączenia pomiędzy miastami w danym państwie wraz z czasem przejazdu. Jest jasne, że nie każdy graf pojawi się tam tak samo często. Po pierwsze, graf ten musi spełniać pewne warunki (jak np. planarność, warunek trójkąta). Po drugie, rzeczywiste sieci dróg spełniają często pewne dodatkowe własności (np. częściej połączone są blisko leżące miasta). Oprócz tego, że grafy występują z różnymi prawdopodobieństwami, to zupełnie nie jest jasne, właściwie z jakimi, jak obliczyć te prawdopodobieństwa. Jest jeszcze inna przyczyna, dla której prawdopodobieństwa dla różnych grafów mogą być bardzo dziwne. Mianowicie, grafy na wejściu mogą być efektem pewnych przekształceń rzeczywistych danych. Może się okazać, że biorą się np. z układów tranzystorów, które przekształcamy na formuły logiczne, a dopiero te formuły na grafy. W takiej sytuacji własności występujących grafów będą bardzo specyficzne. Może się zdarzyć, że w związku z tym algorytm będzie działał dla nich bardzo wolno, pomimo niskiej średniej złożoności. Podsumowując, złożoność średnia jest pożyteczna, ale jednak nie zawsze dobrze odzwierciedla to, czy program jest szybki w praktyce.

Algorytmem, o którym od dawno było wiadomo, że w praktyce działa szybko, ale nie wiadomo właściwie dlaczego, jest algorytm sympleks. Rozwiązuje on problem programowania liniowego, czyli odpowiada na pytanie, czy istnieją takie 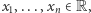które spełniają zbiór ograniczeń liniowych, każde postaci 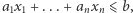tyle, że dla potencjalnie różnych 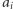oraz 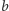(i znajduje wartości 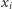). Algorytm sympleks jest bardzo użyteczny przy różnych zagadnieniach optymalizacyjnych i w praktyce naprawdę często stosowany. Co prawda, od dawna znany był algorytm wielomianowy, ale w praktyce stosowany był algorytm sympleks, który ma pesymistyczną złożoność wykładniczą. Aktualnie uważa się, że najlepsze implementacje algorytmu sympleks i jednego z wielomianowych algorytmów (interior-point method) mają podobną efektywność. Jednak przez lata nie wiadomo było, dlaczego sympleks działa tak dobrze, i zostało to wyjaśnione dopiero w pracy Spielmana i Tenga w 2004 roku (za którą otrzymali później prestiżową nagrodę Gödla). Spielman i Teng wprowadzili pojęcie złożoności wygładzonej (smoothed analysis), co do której argumentowali, że jest właściwą miarą szybkości dla algorytmów wczytujących dane rzeczywiste. Następnie pokazali, z grubsza rzecz biorąc, że algorytm sympleks ma sześcienną złożoność wygładzoną, co uzasadnia teoretycznie, dlaczego zachowuje się tak świetnie w praktyce. Cała praca ma 94 strony i jest bardzo skomplikowana technicznie, lecz na uwagę zasługuje proste, ale genialne pojęcie złożoności wygładzonej.

Idea jest podobna jak w złożoności średniej, jednak tu motywacją jest następująca obserwacja. Zauważmy, że jeśli dane do programu pochodzą z urządzeń pomiarowych (co jest częste), to zawsze są nieco zaburzone. Można je uznać za skoncentrowane wokół pewnego punktu (rzeczywistej wartości mierzonej wielkości), dobrym przybliżeniem jest tu wielowymiarowy rozkład normalny o środku w tym punkcie i małej wariancji. Gdybyśmy znali ten punkt, to średni czas działania algorytmu obliczylibyśmy po prostu jako średnią z czasu działania ważoną rozkładem normalnym o środku w tym punkcie. Jako że nie znamy, to przyjmujemy następującą definicję złożoności wygładzonej. Jest to supremum względem wszystkich punktów z przestrzeni ze średniego czasu działania ważonego rozkładem normalnym o środku w tym punkcie i małej wariancji. Jeśli złożoność wygładzona jest mała, to znaczy, że dla dowolnych mierzonych danych średni czas działania programu jest krótki. Czyli sześcienna złożoność wygładzona rzeczywiście dobrze uzasadnia, dlaczego algorytm sympleks w praktyce działa szybko.

Podobną miarę szybkości, oczywiście, można zastosować do innych algorytmów, do których wejściem są liczby rzeczywiste. I rzeczywiście to zrobiono, jest wiele badań na temat złożoności wygładzonej. Wydaje się jednak, że prawdziwe zrozumienie, dlaczego niektóre problemy w teorii trudne są rozwiązywane przez algorytmy w praktyce szybkie, jest dopiero przed nami. Jednym z przykładów jest najbardziej chyba znany problem NP-zupełny: spełnialność formuł logicznych. Jest wiele programów, tzw. SAT-solverów, które w praktyce radzą sobie z nim świetnie. Dlaczego? Myślę, że nikt tego do końca nie wie, ale to już temat na zupełnie inną opowieść.