Zanim przejdziemy do konkretów, potrzebne jest jeszcze jedno doprecyzowanie. Chciałbym już na początku wyraźnie zaznaczyć, że problemy, które będziemy rozważać (i próbować klasyfikować), to wyłącznie problemy decyzyjne, a więc takie, na które odpowiedź to zawsze TAK lub NIE, a nie jakaś liczba czy formuła. A więc interesujący w tym kontekście będzie dla nas problem rozstrzygania, czy dana liczba jest pierwsza czy nie albo czy graf zawiera cykl Hamiltona czy nie. Natomiast w tej definicji nie mieści się problem obliczenia pierwiastków danego równania czy wyznaczenia cyklu Eulera w grafie. Czytelnika Zawiedzionego chciałbym pocieszyć: problemy obliczeniowe zwykle wcale nie są istotnie trudniejsze od decyzyjnych. Nie czas i nie miejsce na mocne uzasadnienie tego zdania, podam tylko przykład: zamiast prosić komputer o znalezienie cyklu Hamiltona dla danego grafu, wystarczy nam program, który rozstrzyga, czy daną ścieżkę da się rozszerzyć do jakiegoś cyklu Hamiltona.

Wróćmy do meritum. Dla komputera (a może raczej: dla informatyka w komputer wyposażonego?) problem decyzyjny jest łatwy, gdy istnieje program, który go zawsze (dla każdych danych) poprawnie rozwiązuje oraz czas działania tego programu można oszacować z góry przez jakiś wielomian z rozmiaru danych. Takim problemem jest chociażby rozstrzyganie, czy podany na wejściu graf zawiera cykl Eulera, albo stwierdzanie, czy opisane równanie kwadratowe ma pierwiastki rzeczywiste. Klasę takich problemów oznaczamy jako P, od angielskiego polynomial.

Spróbujmy przejść oczko wyżej, a więc do prezentacji klasy problemów NP. Nie zacznę od rozwinięcia tego skrótu, wolę bohaterkę przedstawić od innej strony. Moim zdaniem najlepiej jest myśleć o problemach NP jako o problemach, które nie są przynajmniej beznadziejnie trudne (NSPBT, choć krócej jest jednak NP). A problemy NSPBT to dla mnie takie, dla których - o ile odpowiedź brzmi TAK - przynajmniej istnieje podpowiedź, którą gdybyśmy znali (a której znalezienie, być może, jest koszmarnie trudne), to już byśmy umieli łatwo (w sensie już zdefiniowanym) zweryfikować, że odpowiedź faktycznie brzmi TAK. Przykładowo: problem istnienia cyklu Hamiltona jest w NP vel NSPBT. Podpowiedzią jest właśnie wskazanie opisanego cyklu. Łatwo (tym razem: ludzko łatwo) uwierzyć, że samo zweryfikowanie, czy podany cykl jest cyklem Hamiltona w danym grafie, nie jest dla komputera trudne. Podobnie problem spełnialności formuł logicznych: tu podpowiedzią będzie przypisanie zmiennym konkretnych wartości logicznych. I znów: samo sprawdzenie, czy formuła jest prawdziwa przy podanym wartościowaniu jest zadaniem prostym. Oczywiście bynajmniej nie wynika z tego, że problemy decyzyjne: istnienie cyklu Hamiltona w danym grafie czy problem spełnialności formuł są łatwe. Wręcz odwrotnie: podejrzewa się, że nie są one łatwe (nie są w P). Pokazaliśmy tylko, że jeśli odpowiedź jest pozytywna, to istnieje podpowiedź (weryfikator, świadek - różne terminy można znaleźć), która potrafi nas do tego przekonać. Przekonać nas - albo lepiej: udowodnić nam.

Ta ostatnia uwaga jest chyba kluczowa. Bo w tej terminologii możemy wszystko wysłowić jeszcze inaczej: problemy decyzyjne z klasy P to takie, które daje się efektywnie (wielomianowo) rozstrzygać na komputerze. Natomiast problemy z klasy NP to takie, które jeśli mają pozytywną odpowiedź, to jest możliwe uzupełnienie jej DOWODEM, który da się efektywnie zweryfikować. Zauważmy, że druga definicja nie odnosi się do tego, czy znalezienie rzeczonego dowodu jest efektywne. Być może wymaga wykładniczego czasu działania komputera! (Uwaga: z definicji klasy NP wynika, że rozważany dowód nie może być za długi - musi być wielomianowy, bo inaczej nie dałoby się go zweryfikować w czasie wielomianowym.)

Spójrzmy teraz na jeszcze inny problem z klasy NP. Niech wejściem będzie jakaś hipoteza matematyczna H, której zapis ma długość 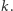Odpowiedzią na problem jest TAK, gdy istnieje dowód matematyczny tej hipotezy o długości nie większej niż 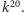Łatwo sprawdzić, że ten problem (oznaczmy go jako X) w istocie jest w NP - świadkiem jest dowód matematyczny hipotezy.

Powoli możemy nabierać intuicji, dlaczego w takim razie nikt nie wierzy, że 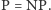Bo przecież gdyby 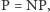to tak naprawdę by oznaczało, że problem X jest też w P. Innymi słowy rozstrzyganie hipotez matematycznych (OK, coś trochę słabszego: rozstrzyganie, czy hipoteza ma dowód krótszy niż jakieś bardzo duże ograniczenie) nie byłoby specjalnie trudniejsze od samego procesu mechanicznej weryfikacji poprawności dowodu!

A w to nie uwierzy chyba nikt, kto choć raz w życiu coś trudnego udowodnił, a końcowy dowód był elegancki i krótki.

Klasa NP ma jeszcze jedną fascynującą własność. Istnieją w niej problemy dowodliwie najtrudniejsze (tzw. zupełne). Problem NP-zupełny to taki, że każdy inny problem z NP można do niego zredukować w czasie wielomianowym. Przykładem problemu NP-zupełnego jest chociażby już omawiany problem cyklu Hamiltona. Oznacza to, że np. każdą instancję H problemu 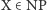długości 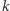da się efektywnie przerobić na pewien graf (rozmiaru wielomianowego od 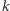) taki, że w tym grafie istnieje cykl Hamiltona wtedy i tylko wtedy, gdy istnieje dowód matematyczny dla hipotezy H długości nie większej niż 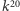! Oczywiście powszechnie wierzy się, że problemy NP-zupełne nie są w P, czyli że są trudne, więc ta konstrukcja niekoniecznie musi być pomocna w dowodzeniu hipotezy H.

PS. Wypada dodać, że oryginalne rozwinięcie skrótu NP, czyli nondeterministic polynomial, odwołuje się do innej (oczywiście równoważnej) definicji klasy NP. Zakładamy w niej, że program działa wielomianowo (czyli szybko), ale może wykonywać niedeterministyczne kroki i zakładać, że "wylosował dobrze". W przypadku problemu X, mógłby napisać losowy ciąg symboli logicznych, po czym sprawdzić, że napisał mu się poprawny dowód.