Informatyczny kącik olimpijski
Jeszcze dwa zadania do plecaka
W kąciku kontynuujemy przygodę z zadaniami, do których rozwiązania przydaje się znajomość problemu plecakowego. Tym razem w nieco trudniejszej jego wersji, w której każdy przedmiot ma swój rozmiar ![|m[i]](/math/temat/informatyka/2015/08/26/Jeszcze_dwa_zadania_do_plecaka/1x-efadbef966d6960db90d9d9f7b6f561c9bdbbd21-im-65,9A,A1-FF,FF,FF.gif) oraz wartość
oraz wartość ![|w[i]:](/math/temat/informatyka/2015/08/26/Jeszcze_dwa_zadania_do_plecaka/2x-efadbef966d6960db90d9d9f7b6f561c9bdbbd21-im-65,9A,A1-FF,FF,FF.gif) Standardowe pytanie, które możemy wtedy zadać, to np. jaka jest największa sumaryczna wartość przedmiotów, które możemy zapakować do plecaka, nie przekraczając jego udźwigu
Standardowe pytanie, które możemy wtedy zadać, to np. jaka jest największa sumaryczna wartość przedmiotów, które możemy zapakować do plecaka, nie przekraczając jego udźwigu 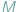
Zacznijmy od zadania Meble z Obozu Naukowo-Treningowego im. A. Kreczmara z roku 2013. Chcemy urządzić mieszkanie i w tym celu zakupiliśmy 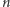 rodzajów mebli do samodzielnego montażu. Mamy
rodzajów mebli do samodzielnego montażu. Mamy 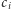 sztuk mebla rodzaju
sztuk mebla rodzaju 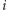 ; złożenie pierwszej sztuki tego rodzaju zajmie nam
; złożenie pierwszej sztuki tego rodzaju zajmie nam 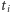 minut, a wraz z postępem prac będziemy nabierać wprawy i złożenie kolejnej sztuki zajmie nam o
minut, a wraz z postępem prac będziemy nabierać wprawy i złożenie kolejnej sztuki zajmie nam o 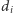 minut krócej niż poprzedniej (zakładamy, że
minut krócej niż poprzedniej (zakładamy, że 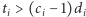 ). Chcemy wiedzieć, ile minimalnie czasu potrzebujemy, aby złożyć dowolnych
). Chcemy wiedzieć, ile minimalnie czasu potrzebujemy, aby złożyć dowolnych 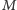 mebli.
mebli.
Naturalne jest tu zastosowanie programowania dynamicznego. Jeśli oznaczymy przez ![dp[i, j]](/math/temat/informatyka/2015/08/26/Jeszcze_dwa_zadania_do_plecaka/1x-e6748ffd13fab73bac0df2e1dcd408f3e414a927-im-33,33,33-FF,FF,FF.gif) minimalny czas złożenia
minimalny czas złożenia 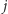 mebli, gdy rozważamy jedynie rodzaje od 1 do
mebli, gdy rozważamy jedynie rodzaje od 1 do 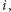 to odpowiedzią będzie
to odpowiedzią będzie ![dp[n, M],](/math/temat/informatyka/2015/08/26/Jeszcze_dwa_zadania_do_plecaka/4x-e6748ffd13fab73bac0df2e1dcd408f3e414a927-im-33,33,33-FF,FF,FF.gif) a rekurencją do niej prowadzącą wzór:
a rekurencją do niej prowadzącą wzór:
![dp[i, j] = min0DkDmin ci, j (dp[i − 1, j −k] + Ti,k),](/math/temat/informatyka/2015/08/26/Jeszcze_dwa_zadania_do_plecaka/5x-e6748ffd13fab73bac0df2e1dcd408f3e414a927-dm-33,33,33-FF,FF,FF.gif) |
gdzie 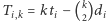 jest czasem montażu
jest czasem montażu 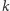 mebli rodzaju
mebli rodzaju 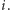 To rozwiązanie działa w czasie
To rozwiązanie działa w czasie 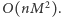
Intuicyjnie rzecz biorąc, jeśli już zaczęliśmy składać meble danego rodzaju, to opłaca się nam wykorzystać zdobyte doświadczenie do maksimum. A formalnie: istnieje optymalne rozwiązanie, w którym mamy co najwyżej jeden rodzaj mebla 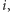 którego złożymy więcej niż 0, ale mniej niż
którego złożymy więcej niż 0, ale mniej niż 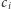 sztuk. Istotnie, załóżmy, że mamy co najmniej dwa takie nietrywialne rodzaje
sztuk. Istotnie, załóżmy, że mamy co najmniej dwa takie nietrywialne rodzaje 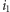 i
i 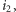 których składamy odpowiednio
których składamy odpowiednio 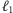 i
i 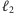 sztuk. Jeśli ostatni mebel rodzaju
sztuk. Jeśli ostatni mebel rodzaju 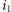 składamy nie dłużej niż ostatni mebel rodzaju
składamy nie dłużej niż ostatni mebel rodzaju 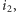 to składając dodatkowe
to składając dodatkowe 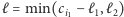 sztuk rodzaju
sztuk rodzaju 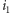 zamiast
zamiast 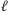 sztuk rodzaju
sztuk rodzaju 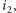 nie pogorszymy czasu, a zmniejszymy liczbę nietrywialnych rodzajów mebli.
nie pogorszymy czasu, a zmniejszymy liczbę nietrywialnych rodzajów mebli.
Rozważmy zatem wszystkie możliwości wyboru nietrywialnego mebla 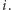 Dla ustalonego
Dla ustalonego 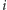 pogrupujmy pozostałe rodzaje mebli
pogrupujmy pozostałe rodzaje mebli 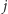 w paczki o rozmiarach
w paczki o rozmiarach ![|m[ j] = c j](/math/temat/informatyka/2015/08/26/Jeszcze_dwa_zadania_do_plecaka/4x-b412e49223e1ef64413eb7f228a4ae017809de38-im-33,33,33-FF,FF,FF.gif) i czasach montażu
i czasach montażu ![w[ j] = T j ,cj](/math/temat/informatyka/2015/08/26/Jeszcze_dwa_zadania_do_plecaka/5x-b412e49223e1ef64413eb7f228a4ae017809de38-im-33,33,33-FF,FF,FF.gif) i rozwiążmy dla nich problem plecakowy, w którym pytamy się o najmniejszą wartość przedmiotów całkowicie wypełniających plecak o udźwigu
i rozwiążmy dla nich problem plecakowy, w którym pytamy się o najmniejszą wartość przedmiotów całkowicie wypełniających plecak o udźwigu 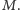 Dzięki temu w czasie
Dzięki temu w czasie 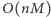 dostaniemy tablicę
dostaniemy tablicę ![d[0..M], |](/math/temat/informatyka/2015/08/26/Jeszcze_dwa_zadania_do_plecaka/8x-b412e49223e1ef64413eb7f228a4ae017809de38-im-33,33,33-FF,FF,FF.gif) w której
w której ![d[j] |](/math/temat/informatyka/2015/08/26/Jeszcze_dwa_zadania_do_plecaka/9x-b412e49223e1ef64413eb7f228a4ae017809de38-im-33,33,33-FF,FF,FF.gif) oznaczać będzie minimalny czas potrzebny na złożenie dokładnie
oznaczać będzie minimalny czas potrzebny na złożenie dokładnie 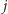 mebli, jeśli pochodzić będą z pewnej liczby w całości złożonych paczek. Zatem, dokładając do tego
mebli, jeśli pochodzić będą z pewnej liczby w całości złożonych paczek. Zatem, dokładając do tego 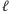 sztuk mebla
sztuk mebla 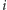 (dla wszystkich wartości
(dla wszystkich wartości 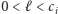 ), zmontujemy
), zmontujemy 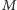 mebli w czasie
mebli w czasie 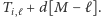 Złożoność czasowa tego rozwiązania to
Złożoność czasowa tego rozwiązania to 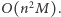
Zauważmy, że główny koszt algorytmu to rozwiązanie problemu plecakowego dla każdego podzbioru 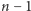 przedmiotów. Używając techniki, o której pisaliśmy w zeszłym miesiącu, możemy zmniejszyć złożoność czasową do
przedmiotów. Używając techniki, o której pisaliśmy w zeszłym miesiącu, możemy zmniejszyć złożoność czasową do 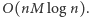
Drugie zadanie pochodzi z Wiosennego Turnieju w Programowaniu Zespołowym organizowanego przez Politechnikę Poznańską (a konkretnie z 8. edycji z roku 2004) i ma tytuł (kto by się spodziewał) Pakowanie plecaka. W zadaniu mamy plecak o udźwigu 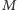 i
i  przedmiotów, z których każdy ma swój rozmiar
przedmiotów, z których każdy ma swój rozmiar ![m[i]](/math/temat/informatyka/2015/08/26/Jeszcze_dwa_zadania_do_plecaka/3x-08fbdc94ec9adfbd9c7f3655cdc124b93cfe8c2b-im-33,33,33-FF,FF,FF.gif) oraz użyteczność
oraz użyteczność ![|w[i]](/math/temat/informatyka/2015/08/26/Jeszcze_dwa_zadania_do_plecaka/4x-08fbdc94ec9adfbd9c7f3655cdc124b93cfe8c2b-im-33,33,33-FF,FF,FF.gif) (przy czym niektóre przedmioty mogą być wyjątkowo nieprzydatne i mieć ujemną użyteczność). Chcemy znaleźć maksymalne upakowanie plecaka (tzn. takie, do którego nie będzie można dołożyć żadnego przedmiotu) o największej sumie użyteczności zabranych przedmiotów (zatem, być może, będziemy zmuszeni zabrać jakiś nieprzydatny przedmiot tylko po to, by dociążyć plecak).
(przy czym niektóre przedmioty mogą być wyjątkowo nieprzydatne i mieć ujemną użyteczność). Chcemy znaleźć maksymalne upakowanie plecaka (tzn. takie, do którego nie będzie można dołożyć żadnego przedmiotu) o największej sumie użyteczności zabranych przedmiotów (zatem, być może, będziemy zmuszeni zabrać jakiś nieprzydatny przedmiot tylko po to, by dociążyć plecak).
Zauważmy, że jeśli będziemy chcieli zostawić w plecaku puste miejsce o wielkości 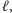 to wszystkie przedmioty o rozmiarach nie większych niż
to wszystkie przedmioty o rozmiarach nie większych niż 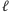 będą musiały znaleźć się w plecaku (inaczej moglibyśmy dołożyć do plecaka co najmniej jeden z nich). Posortujmy zatem przedmioty względem ich rozmiarów i podzielmy na grupę
będą musiały znaleźć się w plecaku (inaczej moglibyśmy dołożyć do plecaka co najmniej jeden z nich). Posortujmy zatem przedmioty względem ich rozmiarów i podzielmy na grupę 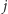 przedmiotów "dużych" i
przedmiotów "dużych" i 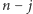 przedmiotów "małych", co po ewentualnym przenumerowaniu przedmiotów da nam
przedmiotów "małych", co po ewentualnym przenumerowaniu przedmiotów da nam
![w[1]⩾ w[2] ⩾...⩾ w[ j] > ℓ ⩾ w[ j + 1] ⩾ ... ⩾w[n].](/math/temat/informatyka/2015/08/26/Jeszcze_dwa_zadania_do_plecaka/5x-a34ecb95d188983bb6bbb552731653c1f7926708-dm-33,33,33-FF,FF,FF.gif)
Do plecaka na pewno weźmiemy wszystkie "małe" przedmioty o łącznym rozmiarze ![m⋆ = PiA jm[i]](/math/temat/informatyka/2015/08/26/Jeszcze_dwa_zadania_do_plecaka/6x-a34ecb95d188983bb6bbb552731653c1f7926708-im-33,33,33-FF,FF,FF.gif) i użyteczności
i użyteczności ![w⋆ = PiAj w[i].](/math/temat/informatyka/2015/08/26/Jeszcze_dwa_zadania_do_plecaka/7x-a34ecb95d188983bb6bbb552731653c1f7926708-im-33,33,33-FF,FF,FF.gif) Pozostałe przedmioty muszą zająć w plecaku miejsce o wielkości dokładnie
Pozostałe przedmioty muszą zająć w plecaku miejsce o wielkości dokładnie 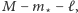 ale poza tym możemy je wybrać dowolnie. Zatem wystarczy, że rozwiążemy dla nich problem plecakowy maksymalizujący wartość zabranych przedmiotów - odpowiedzią będzie
ale poza tym możemy je wybrać dowolnie. Zatem wystarczy, że rozwiążemy dla nich problem plecakowy maksymalizujący wartość zabranych przedmiotów - odpowiedzią będzie 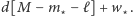
Jeśli przeiterujemy po wartościach 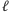 w kolejności malejącej, to każdy przedmiot dokładnie raz zmieni swój status z "małego" na "duży". Możemy więc na bieżąco rozwiązywać problem plecakowy i uaktualniać wartości
w kolejności malejącej, to każdy przedmiot dokładnie raz zmieni swój status z "małego" na "duży". Możemy więc na bieżąco rozwiązywać problem plecakowy i uaktualniać wartości 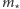 i
i 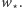 Wtedy koszt każdej takiej zmiany wyniesie
Wtedy koszt każdej takiej zmiany wyniesie 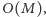 a cały algorytm będzie miał złożoność czasową
a cały algorytm będzie miał złożoność czasową