Informatyczny kącik olimpijski
Wypisz napis
W tym kąciku omówimy pierwsze zadanie z finału konkursu Google Code Jam 2010.
Zadanie 1. Naszym celem jest wypisanie kolejno liter tego napisu od lewej
do prawej. Mamy do dyspozycji stempel, który możemy wyobrazić sobie
jako stos, umożliwiający wykonywanie trzech typów operacji: doczepienie
plakietki z literą
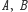 lub
lub
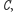 odczepienie plakietki znajdującej
się na wierzchu oraz przyłożenie stempla do kartki, w wyniku czego
nadrukowuje się na niej litera z wierzchniej plakietki. Chcemy wypisać
odczepienie plakietki znajdującej
się na wierzchu oraz przyłożenie stempla do kartki, w wyniku czego
nadrukowuje się na niej litera z wierzchniej plakietki. Chcemy wypisać
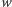 za pomocą najmniejszej możliwej liczby operacji, przy czym
zaczynamy i kończymy z pustym stemplem (stosem).
za pomocą najmniejszej możliwej liczby operacji, przy czym
zaczynamy i kończymy z pustym stemplem (stosem).
Jednym z pierwszych pomysłów na rozwiązanie może być programowanie
dynamiczne. Wyznaczamy w nim kolejne komórki tablicy
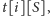 oznaczające,
w jakiej minimalnej liczbie operacji można wypisać początkowy fragment
napisu,
oznaczające,
w jakiej minimalnej liczbie operacji można wypisać początkowy fragment
napisu,
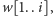 tak aby na końcu otrzymać stos reprezentowany przez
napis
tak aby na końcu otrzymać stos reprezentowany przez
napis
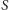 (nad alfabetem
(nad alfabetem
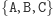 ). Wynikiem jest wówczas
). Wynikiem jest wówczas
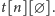 Przy tym podejściu nieuchronnie napotykamy problem, że
liczba możliwych stosów jest naprawdę duża. Zauważmy, że nigdy
na stosie nie opłaca nam się trzymać więcej niż
Przy tym podejściu nieuchronnie napotykamy problem, że
liczba możliwych stosów jest naprawdę duża. Zauważmy, że nigdy
na stosie nie opłaca nam się trzymać więcej niż
 liter, gdyż
wówczas musielibyśmy łącznie wykonać ponad
liter, gdyż
wówczas musielibyśmy łącznie wykonać ponad
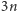 operacji, a w
operacji, a w
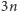 operacjach naprawdę łatwo wypisać cały napis
operacjach naprawdę łatwo wypisać cały napis
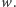 Czyli mamy
co najwyżej
Czyli mamy
co najwyżej
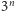 różnych stosów, ale do tego jeszcze mnóstwo
możliwych przejść z każdego stanu
różnych stosów, ale do tego jeszcze mnóstwo
możliwych przejść z każdego stanu
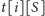 do stanów postaci
do stanów postaci
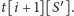
Pokażemy teraz, jak trochę polepszyć to rozwiązanie. Przede wszystkim
na stosie ewidentnie nie opłaca się nigdy trzymać dwóch takich
samych liter pod rząd. To redukuje liczbę interesujących nas stosów do
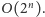 Możemy też istotnie zmniejszyć liczbę rozważanych
przejść, jeśli zauważymy, że w danym stanie wystarczy próbować
dołożyć na stos co najwyżej jedną nową literkę. Skrótowe uzasadnienie na
przykładzie: zamiast w danym stanie dokładać na stos literki
Możemy też istotnie zmniejszyć liczbę rozważanych
przejść, jeśli zauważymy, że w danym stanie wystarczy próbować
dołożyć na stos co najwyżej jedną nową literkę. Skrótowe uzasadnienie na
przykładzie: zamiast w danym stanie dokładać na stos literki
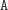
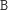 ,
wystarczy dołożyć samą literkę
,
wystarczy dołożyć samą literkę
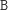 . Jeśli potem, po zdjęciu
. Jeśli potem, po zdjęciu
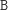 ,
będę chciał użyć tego
,
będę chciał użyć tego
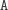 , którego nie dołożyłem, to dokładam
to
, którego nie dołożyłem, to dokładam
to
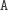 właśnie wtedy. Liczba operacji nie zwiększyła się, a postąpiłem
jakby sprytniej. W ten sposób zmniejszyliśmy liczbę przejść z danego
stanu do
właśnie wtedy. Liczba operacji nie zwiększyła się, a postąpiłem
jakby sprytniej. W ten sposób zmniejszyliśmy liczbę przejść z danego
stanu do
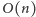 (dodanie co najwyżej jednej literki i usunięcie
dowolnie wielu literek), co daje już rozwiązanie o koszcie czasowym
(dodanie co najwyżej jednej literki i usunięcie
dowolnie wielu literek), co daje już rozwiązanie o koszcie czasowym
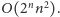 Wyraźnie lepiej niż poprzednio, ale wciąż jakoś wolno.
Wyraźnie lepiej niż poprzednio, ale wciąż jakoś wolno.
Spróbujmy więc zmienić podejście do rozwiązania. Przyjrzyjmy się
sytuacji początkowej. Zaczynamy od pustego stosu, a chcemy wypisać
literkę
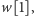 więc musimy ją włożyć na stos. Oznaczmy przez
więc musimy ją włożyć na stos. Oznaczmy przez
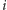 „moment”, po którym
„moment”, po którym
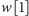 zostanie zdjęte ze stosu,
tzn. załóżmy, że
zostanie zdjęte ze stosu,
tzn. załóżmy, że
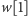 znajduje się na spodzie stosu podczas
wypisywania liter fragmentu
znajduje się na spodzie stosu podczas
wypisywania liter fragmentu
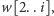 po czym zostaje zdjęte ze stosu
(
po czym zostaje zdjęte ze stosu
(
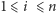 ). Podzieliliśmy zatem wyjściowy problem na dwa
niezależne podproblemy, polegające na wypisaniu każdego z fragmentów
). Podzieliliśmy zatem wyjściowy problem na dwa
niezależne podproblemy, polegające na wypisaniu każdego z fragmentów
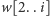 oraz
oraz
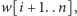 tak aby na końcu zdjąć ze stosu
wszystkie dołożone po drodze litery. Jedyna różnica między podproblemami
polega na tym, że podczas wypisywania
tak aby na końcu zdjąć ze stosu
wszystkie dołożone po drodze litery. Jedyna różnica między podproblemami
polega na tym, że podczas wypisywania
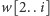 możemy skorzystać
z faktu, iż na stosie jest już litera
możemy skorzystać
z faktu, iż na stosie jest już litera
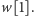 To prowadzi nas do
innego rozwiązania opartego na programowaniu dynamicznym. Przez
To prowadzi nas do
innego rozwiązania opartego na programowaniu dynamicznym. Przez
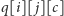 oznaczmy minimalną liczbę operacji potrzebnych do
wypisania fragmentu
oznaczmy minimalną liczbę operacji potrzebnych do
wypisania fragmentu
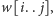 tak aby nie pozostawić na końcu
żadnych dodatkowych liter na stosie. A to wszystko przy założeniu, że na
szczycie stosu przed rozważeniem tego fragmentu znajduje się literka
tak aby nie pozostawić na końcu
żadnych dodatkowych liter na stosie. A to wszystko przy założeniu, że na
szczycie stosu przed rozważeniem tego fragmentu znajduje się literka
 ;
;
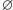 oznacza, że przed rozpoczęciem wypisywania
oznacza, że przed rozpoczęciem wypisywania
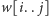 stos był pusty. Dodajmy dla jasności, że literki
stos był pusty. Dodajmy dla jasności, że literki
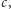 ani
niczego poniżej, nie możemy tu usunąć ze stosu. Przykładowo, wartości
postaci
ani
niczego poniżej, nie możemy tu usunąć ze stosu. Przykładowo, wartości
postaci
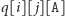 obliczamy następująco: jeśli
obliczamy następująco: jeśli
 to
to
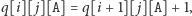 a w przeciwnym razie
a w przeciwnym razie
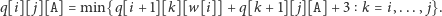
Przy tym
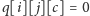 dla
dla
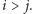 Takie rozwiązanie ma
złożoność czasową
Takie rozwiązanie ma
złożoność czasową
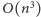 – pozwalało to zdobyć częściowe punkty
na zawodach.
– pozwalało to zdobyć częściowe punkty
na zawodach.
Istnieje zatem jeszcze lepsze rozwiązanie. Co ciekawe, aby je uzyskać, należy
wrócić do poprzedniego, wykładniczego rozwiązania, i jeszcze dokładniej
przyjrzeć się możliwym zawartościom stosu. Kluczowa obserwacja
to: można nie rozważać stosów, w których występuje fragment
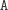
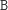
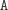 . Faktycznie, rozważmy rozwiązanie, w którym na
stosie pojawia się fragment tej postaci, i przyjrzyjmy się chwili, w której
umieszczamy na stosie drugą z literek
. Faktycznie, rozważmy rozwiązanie, w którym na
stosie pojawia się fragment tej postaci, i przyjrzyjmy się chwili, w której
umieszczamy na stosie drugą z literek
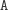 . Zróbmy jednak inaczej: zamiast
umieszczać drugie
. Zróbmy jednak inaczej: zamiast
umieszczać drugie
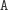 , usuńmy ze stosu literkę
, usuńmy ze stosu literkę
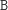 . Liczba operacji
nie zmieniła się, a na szczycie stosu wciąż mamy
. Liczba operacji
nie zmieniła się, a na szczycie stosu wciąż mamy
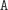 . Dalej wykonujemy
rozwiązanie bez zmian, aż do chwili, w której próbuje ono zdjąć ze
stosu to drugie
. Dalej wykonujemy
rozwiązanie bez zmian, aż do chwili, w której próbuje ono zdjąć ze
stosu to drugie
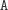 , którego teraz nie ma. W zamian włóżmy
na stos literkę
, którego teraz nie ma. W zamian włóżmy
na stos literkę
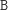 . Liczba operacji nie zmieniła się, układ liter na
stosie również. W ten sposób pozbyliśmy się jednego wystąpienia
fragmentu
. Liczba operacji nie zmieniła się, układ liter na
stosie również. W ten sposób pozbyliśmy się jednego wystąpienia
fragmentu
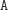
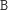
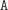 ; jeśli jest ich więcej, eliminujemy je
w ten sam sposób.
; jeśli jest ich więcej, eliminujemy je
w ten sam sposób.
Podobnie można uzasadnić, że możemy nie rozważać stosów zawierających
fragment
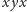 dla dowolnych, różnych liter
dla dowolnych, różnych liter
 i
i
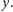 Stosów
bez takich napisów jest już bardzo mało: są to tylko stosy postaci
Stosów
bez takich napisów jest już bardzo mało: są to tylko stosy postaci
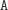
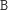
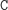
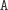
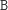
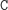 ...,
...,
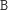
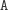
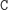
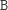
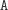
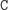 ...
i jeszcze czterech innych (dowolna permutacja liter
...
i jeszcze czterech innych (dowolna permutacja liter
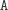 ,
,
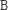 ,
,
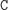 na początku).
Tak oto tablica
na początku).
Tak oto tablica
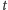 skurczyła się nam do rozmiaru
skurczyła się nam do rozmiaru
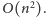 Wreszcie
liczbę przejść z każdego stanu możemy zmniejszyć do stałej, korzystając ze
spostrzeżenia, że jeśli przy wypisywaniu
Wreszcie
liczbę przejść z każdego stanu możemy zmniejszyć do stałej, korzystając ze
spostrzeżenia, że jeśli przy wypisywaniu
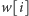 decydujemy się na
usuwanie liter ze stosu, to możemy to robić do chwili, gdy po raz pierwszy
na szczycie stosu znajdzie się litera
decydujemy się na
usuwanie liter ze stosu, to możemy to robić do chwili, gdy po raz pierwszy
na szczycie stosu znajdzie się litera
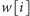 lub gdy stos stanie się
pusty. To oznacza, że w danym stanie usuniemy ze stosu co najwyżej
dwie literki (lub wszystkie) i dodamy na stos co najwyżej jedną. W ten
sposób uzyskaliśmy rozwiązanie wzorcowe, o złożoności czasowej
lub gdy stos stanie się
pusty. To oznacza, że w danym stanie usuniemy ze stosu co najwyżej
dwie literki (lub wszystkie) i dodamy na stos co najwyżej jedną. W ten
sposób uzyskaliśmy rozwiązanie wzorcowe, o złożoności czasowej