Trochę zagmatwaną treść zadania można streścić w następujący sposób: mamy dany -wierzchołkowy graf nieskierowany 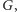 w którym każdy z wierzchołków utożsamiamy z pewnym, zadanym punktem na płaszczyźnie. Stopień każdego wierzchołka (czyli liczba krawędzi z nim incydentnych) to 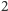 lub 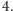 Naszym zadaniem jest znaleźć taki cykl Eulera w 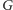 (tj. cykl, który przechodzi każdą krawędzią dokładnie raz), którego koszt jest minimalny. Kosztem cyklu nazywamy sumę kątów pomiędzy każdą parą kolejnych krawędzi cyklu, przy czym interesują nas najmniejsze kąty pomiędzy prostymi zawierającymi pary kolejnych krawędzi.

Najprostszym rozwiązaniem jest przejrzenie wszystkich możliwości połączeń par krawędzi w każdym wierzchołku stopnia 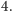 Dla każdego układu połączeń sprawdzamy, czy tworzy on cykl Eulera, a jeśli tak, to obliczamy jego koszt. Niestety, takie rozwiązanie ma złożoność czasową 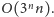 Tak od razu nie widać metody na szybkie znalezienie najtańszego cyklu Eulera, podejdźmy zatem do problemu od innej strony. Możemy, na przykład, spróbować stworzyć jakikolwiek cykl Eulera, a później stopniowo zmniejszać jego sumaryczny koszt. Autor tego kącika nie ma jednak pomysłu na szybkie rozwiązanie problemu tym sposobem.

Podejście odwrotne daje natomiast rezultaty. Spróbujmy utworzyć ze wszystkich krawędzi grafu 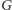 możliwie najtańszy zbiór cykli, a później najmniejszym kosztem pozmieniać połączenia w poszczególnych wierzchołkach tak, by powstał cykl Eulera. Na początku w każdym wierzchołku stopnia  łączymy krawędzie w pary tak, aby suma kosztów była jak najmniejsza. W ten sposób otrzymujemy zbiór cykli 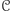 o minimalnym możliwym koszcie. Zauważmy teraz, że jeśli dwa cykle 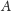 i 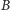 z tego zbioru przechodzą przez ten sam wierzchołek 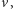 to – poprzez dowolną zamianę połączeń w wierzchołku  na inne – łączymy te dwa cykle w jeden. Oznaczmy minimalny koszt takiej zmiany w wierzchołku  przez 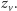 Jeśli zaś zmienimy połączenia w wierzchołku, który należy do jednego cyklu (przy czym cykl przechodzi przez niego dwukrotnie), to albo nic się nie zmieni, albo podzielimy tenże cykl na dwa.

Stwórzmy teraz nowy multigraf 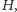 w którym wierzchołkami są cykle ze zbioru 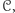 a krawędziami wierzchołki stopnia 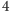 z 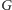 – przez każdy taki wierzchołek przechodzą wszakże dokładnie dwa cykle (niekoniecznie różne). Kosztem krawędzi odpowiadającej wierzchołkowi  z 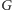 niech będzie 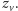 Szukamy najtańszego sposobu połączenia wszystkich cykli w jeden, ale w multigrafie 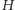 odpowiada to szukaniu zbioru krawędzi o minimalnym koszcie łączącego wszystkie wierzchołki. Jest to zatem problem wyznaczenia najtańszego drzewa rozpinającego w 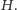 Zauważmy, że gdyby krawędzie 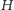 mogły mieć ujemne koszty, to takie rozwiązanie nie działałoby, gdyż, być może, opłacałoby się wybrać, poza drzewem rozpinającym, jeszcze trochę krawędzi z 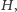 które zmniejszyłyby koszt. U nas jednak 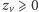 dla każdego wierzchołka  z 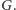 Znanych jest kilka efektywnych algorytmów znajdujących minimalne drzewo rozpinające, np. 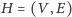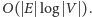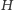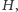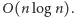algorytmy Kruskala i Prima, działające dla grafu  w czasie  Całe rozwiązanie zadania wymaga zbudowania grafu  (koszt liniowy), a następnie znalezienia minimalnego drzewa rozpinającego w  co możemy wykonać w czasie  Takie rozwiązanie w żaden sposób nie korzysta ze specyfiki danych wejściowych, w szczególności z geometrycznych własności grafu oraz sposobu obliczania kosztów. Autor nie zna rozwiązania, które w istotny sposób korzystałoby z tych informacji, zachęca więc Czytelnika do próby znalezienia takowego.