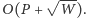Informatyczny kącik olimpijski
Wieże
W tym kąciku zajmiemy się rozwiązaniem zadania pochodzącego z jednej z finałowych rund konkursu TopCoder Open 2010, o nazwie Shrooks on the Board.

Zadanie. Jesteśmy proszeni o obliczenie reszty
z dzielenia liczby poprawnych ustawień wież na planszy przez zadaną
liczbę pierwszą
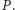 Plansza jest prostokątna, ma
Plansza jest prostokątna, ma
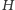 wierszy oraz
wierszy oraz
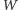 kolumn. W tym zadaniu wieże są nietypowe: atakują jedynie
pola znajdujące się w tym samym wierszu i do tego odległe o co najwyżej
kolumn. W tym zadaniu wieże są nietypowe: atakują jedynie
pola znajdujące się w tym samym wierszu i do tego odległe o co najwyżej
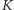 pól. Poprawne ustawienie to takie, które zawiera co najmniej
jedną wieżę i żadna wieża nie atakuje innej.
pól. Poprawne ustawienie to takie, które zawiera co najmniej
jedną wieżę i żadna wieża nie atakuje innej.
Zauważmy na początek, że istnieje dokładnie jedno ustawienie, które
nie zawiera wież. Będziemy uznawali je za poprawne, a na końcu wynik
zmniejszymy o 1. Możemy więc ustawić dowolną liczbę wież w dowolny
sposób, byle się nie atakowały. Od tej pory problemy dla poszczególnych
wierszy są niezależne. Łatwo zauważyć, że jeżeli wieże w jednym wierszu
można ustawić na
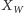 sposobów, to ostatecznym wynikiem będzie
reszta z dzielenia liczby
sposobów, to ostatecznym wynikiem będzie
reszta z dzielenia liczby
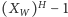 przez
przez
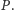 Do obliczenia tejże
reszty wystarczy znać resztę z dzielenia liczby
Do obliczenia tejże
reszty wystarczy znać resztę z dzielenia liczby
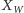 przez
przez
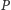 ; koszt
czasowy końcowego potęgowania to
; koszt
czasowy końcowego potęgowania to
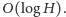
Cały problem polega więc na wyznaczeniu wartości
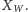 Spróbujmy
najpierw wyprowadzić wzór rekurencyjny na
Spróbujmy
najpierw wyprowadzić wzór rekurencyjny na
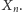 Mamy następujące
możliwości: albo pierwsze pole jest puste, a dalsza część planszy jest jakoś
zapełniona wieżami, co daje
Mamy następujące
możliwości: albo pierwsze pole jest puste, a dalsza część planszy jest jakoś
zapełniona wieżami, co daje
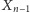 poprawnych ustawień, albo też na
pierwszym polu stoi wieża, kolejne
poprawnych ustawień, albo też na
pierwszym polu stoi wieża, kolejne
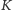 pól jest pustych, a pozostałe są
jakoś zapełnione, co daje dodatkowe
pól jest pustych, a pozostałe są
jakoś zapełnione, co daje dodatkowe
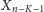 ustawień. Ostatecznie
mamy, że
ustawień. Ostatecznie
mamy, że
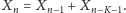 Pozostaje zaznaczyć, iż dla
Pozostaje zaznaczyć, iż dla
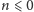 przyjmujemy
przyjmujemy
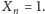 Daje to prosty algorytm obliczający
Daje to prosty algorytm obliczający
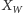 w czasie
w czasie
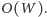
Inne rozwiązanie otrzymujemy, stosując standardową metodę obliczania wyrazów ciągu zadanego wzorem rekurencyjnym za pomocą szybkiego potęgowania macierzy, patrz artykuł Macierze oczami informatyka w Delcie 7/2009. Przypomnijmy tylko, że w metodzie tej przedstawiamy taki oto wektor

jako iloczyn pewnej macierzy
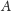 rozmiaru
rozmiaru
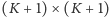 i analogicznego wektora zapisanego dla
i analogicznego wektora zapisanego dla
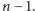 Wówczas zadanie
sprowadza się do obliczenia macierzy
Wówczas zadanie
sprowadza się do obliczenia macierzy
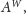 co możemy wykonać
w czasie
co możemy wykonać
w czasie
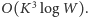
Spróbujmy teraz podejść do problemu od innej strony. Pokażemy, że
sposobów ustawienia
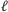 wież w wierszu długości
wież w wierszu długości
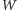 jest tyle
samo, co wyborów
jest tyle
samo, co wyborów
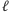 elementów spośród
elementów spośród
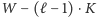 elementów. Dla ustalenia uwagi przyjmijmy, że wieża zajmuje swoje
pole oraz
elementów. Dla ustalenia uwagi przyjmijmy, że wieża zajmuje swoje
pole oraz
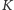 pól na prawo od niego. W takim razie możemy
skonstruować bijekcję między ustawieniami wież a wyborami elementów.
Mając dane ustawienie wież, po prostu usuwamy
pól na prawo od niego. W takim razie możemy
skonstruować bijekcję między ustawieniami wież a wyborami elementów.
Mając dane ustawienie wież, po prostu usuwamy
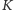 pól na prawo
od każdej wieży poza ostatnią i otrzymujemy wybór
pól na prawo
od każdej wieży poza ostatnią i otrzymujemy wybór
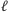 pól
spośród
pól
spośród
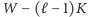 pól. Odwrotnie, mając dany pewien wybór
pól. Odwrotnie, mając dany pewien wybór
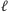 elementów spośród
elementów spośród
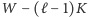 elementów, ustawiamy
wieże w polach odpowiadających tym elementom i po każdej (poza ostatnią)
dokładamy dodatkowo
elementów, ustawiamy
wieże w polach odpowiadających tym elementom i po każdej (poza ostatnią)
dokładamy dodatkowo
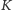 wolnych pól.
wolnych pól.
Żądanych ustawień wież jest zatem
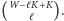 Oczywiście, musi
być
Oczywiście, musi
być
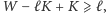 czyli
czyli
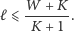
Aby obliczyć resztę z dzielenia
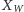 przez
przez
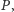 wystarczy umieć
szybko obliczać reszty z dzielenia symboli Newtona przez
wystarczy umieć
szybko obliczać reszty z dzielenia symboli Newtona przez
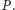 W tym celu
korzystamy z twierdzenia Lucasa, które orzeka, że jeśli
W tym celu
korzystamy z twierdzenia Lucasa, które orzeka, że jeśli
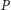 jest liczbą
pierwszą i
jest liczbą
pierwszą i
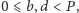 to
to
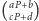 daje taką samą resztę z dzielenia
przez
daje taką samą resztę z dzielenia
przez
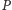 co
co
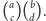 Zauważmy teraz, że zarówno reszty
z dzielenia liczb
Zauważmy teraz, że zarówno reszty
z dzielenia liczb
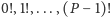 przez
przez
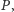 jak i ich odwrotności
modulo
jak i ich odwrotności
modulo
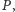 możemy obliczyć w czasie
możemy obliczyć w czasie
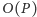 – te drugie według
wzorów
– te drugie według
wzorów
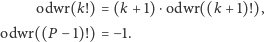
Wówczas resztę z dzielenia
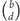 przez
przez
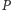 obliczamy w czasie
stałym, natomiast
obliczamy w czasie
stałym, natomiast
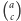 ponownie zapisujemy w postaci
ponownie zapisujemy w postaci
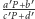 i zaczynamy od początku. W ten sposób symbol Newtona
i zaczynamy od początku. W ten sposób symbol Newtona
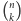 obliczamy
w czasie
obliczamy
w czasie
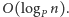 Możemy więc obliczyć
Możemy więc obliczyć
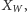 wykonując
wykonując
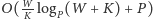 operacji. Można śmiało powiedzieć, że jest to
operacji. Można śmiało powiedzieć, że jest to
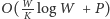 operacji, gdyż
operacji, gdyż
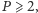 a zadanie jest interesujące
tylko dla
a zadanie jest interesujące
tylko dla
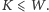
Żadne z powyższych rozwiązań nie jest jeszcze satysfakcjonujące.
Aby uzyskać lepszy wynik, połączymy ostatnie dwa rozwiązania. Jeśli
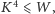 to uruchamiamy rozwiązanie z mnożeniem macierzy,
a w przeciwnym przypadku rozwiązanie przez symbole Newtona. Ostatecznie,
całe zadanie rozwiązujemy w czasie
to uruchamiamy rozwiązanie z mnożeniem macierzy,
a w przeciwnym przypadku rozwiązanie przez symbole Newtona. Ostatecznie,
całe zadanie rozwiązujemy w czasie
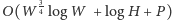 przy
zużyciu pamięci rzędu
przy
zużyciu pamięci rzędu