Co to jest?
Nowe pomysły
Sieć optyczna - kryształ doskonały
Sieci optyczne są nowym materiałem, będącym cały czas przedmiotem aktywnych badań. W ostatnich latach bardzo szybko pojawiają się nowe możliwości eksperymentalne, rozwijana jest teoria. Można je zastosować do badania mechanizmów fizyki ciała stałego.
W 1913 roku Niels Bohr zapostulował model atomu wodoru. W tym modelu
układ protonu i elektronu nie może mieć dowolnej energii wiązania, lecz musi
ona wynosić
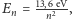 dla
dla
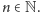 Przeskok między poziomami
Przeskok między poziomami
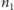 i
i
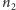 jest powiązany z absorpcją lub emisją fotonu o energii
jest powiązany z absorpcją lub emisją fotonu o energii
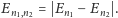 Zbiór wszystkich liczb
Zbiór wszystkich liczb
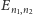 tworzy tzw.
widmo, czyli zbiór wartości energii fotonów, które atom może emitować
lub absorbować. Foton o energii
tworzy tzw.
widmo, czyli zbiór wartości energii fotonów, które atom może emitować
lub absorbować. Foton o energii
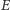 ma określoną częstotliwość:
ma określoną częstotliwość:
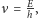 gdzie
gdzie
 jest stałą Plancka.
jest stałą Plancka.
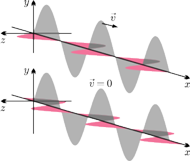
Rys. 1 Fala elektromagnetyczna opisana równaniami (4)–(5). W górnym wierszu fala biegnąca (maksima przesuwają się wzdłuż osi), w dolnym stojąca (maksima wykonują ruch góra-dół, nie przemieszczają się wzdłuż osi).
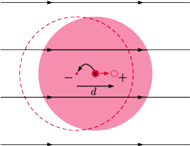
Rys. 2 Indukcja momentu dipolowego przez jednorodne pole elektryczne.
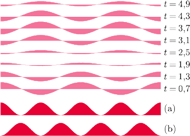
Rys. 3 Jasnym kolorem zaznaczono pole
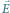 fali stojącej dla różnych
fali stojącej dla różnych
 (dla
(dla
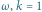 ). Jeśli mianownik w równaniu (5) jest dodatni, to
). Jeśli mianownik w równaniu (5) jest dodatni, to
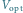 jest postaci (a),
jest natomiast postaci (b), jeśli jest ujemny.
jest postaci (a),
jest natomiast postaci (b), jeśli jest ujemny.
Inne pierwiastki mają więcej elektronów, tym samym mają bardziej skomplikowane widma, bardzo trudne do obliczenia nawet w przybliżeniu. Widma (nawet wodoru) komplikują też nieuwzględnione efekty (choćby relatywistyczne). Widma atomów, wyznaczone doświadczalnie lub obliczone komputerowo, są w dużej mierze skatalogowane w ogólnodostępnych źródłach.
Z klasycznego punktu widzenia światło (w tym wiązka lasera) jest falą
elektromagnetyczną, którą opisują równania Maxwella. W układzie
odniesienia, takim że wiązka propaguje się wzdłuż osi
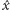 w prawo
(Rys. 1), falę tę można opisać jako układ pól elektrycznego i magnetycznego
zmiennych w czasie i przestrzeni:
w prawo
(Rys. 1), falę tę można opisać jako układ pól elektrycznego i magnetycznego
zmiennych w czasie i przestrzeni:
gdzie
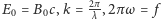 oraz
oraz
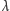 jest długością fali, a
jest długością fali, a
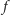 jej częstotliwością. Założenie, że
jej częstotliwością. Założenie, że
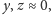 bierze się stąd, iż
powyższe równania opisują jedynie światło wewnątrz wiązki. Jeśli zestawimy
dwie wiązki powyższego typu, propagujące wzdłuż osi
bierze się stąd, iż
powyższe równania opisują jedynie światło wewnątrz wiązki. Jeśli zestawimy
dwie wiązki powyższego typu, propagujące wzdłuż osi
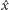 w przeciwne
strony (tak by wektory
w przeciwne
strony (tak by wektory
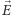 leżały na jednej płaszczyźnie), otrzymamy falę
stojącą:
leżały na jednej płaszczyźnie), otrzymamy falę
stojącą:
Opisaliśmy przypadek oddziaływania atomu z fotonami o energiach
odpowiadających energiom przejścia między poziomami energetycznymi.
Jeśli atom znajduje się w polu elektromagnetycznym, które jest falą
stojącą o takiej częstotliwości
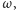 że nie odpowiada ona żadnej
z częstotliwości przejścia atomowego, wówczas emisja i absorpcja fotonów
jest niesłychanie rzadka (w skali zjawisk atomowych) i pomijalna. Z drugiej
strony, atom, znajdując się w polu elektrycznym, polaryzuje się (jądro
przyciągane jest w przeciwną stronę niż chmura elektronów, indukowany
jest moment dipolowy
że nie odpowiada ona żadnej
z częstotliwości przejścia atomowego, wówczas emisja i absorpcja fotonów
jest niesłychanie rzadka (w skali zjawisk atomowych) i pomijalna. Z drugiej
strony, atom, znajdując się w polu elektrycznym, polaryzuje się (jądro
przyciągane jest w przeciwną stronę niż chmura elektronów, indukowany
jest moment dipolowy
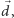 co powoduje zmianę energii atomu o
co powoduje zmianę energii atomu o
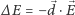 ).
).
Gdy pole elektryczne pochodzi od fali stojącej, której częstotliwość
odpowiada fotonom o energii bliskiej różnicy energii między pewnymi dwoma
poziomami
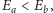 okazuje się, że:
okazuje się, że:
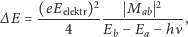 | (5) |
gdzie
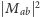 jest proporcjonalne do prawdopodobieństwa przejścia
między poziomami
jest proporcjonalne do prawdopodobieństwa przejścia
między poziomami
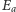 i
i
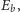 gdyby takowe mogło zajść,
gdyby takowe mogło zajść,
 jest wartością ładunku elektronu, a
jest wartością ładunku elektronu, a
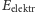 jest amplitudą
elektrycznej składowej fali stojącej w danym punkcie przestrzeni – u nas
jest amplitudą
elektrycznej składowej fali stojącej w danym punkcie przestrzeni – u nas
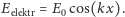 W praktyce „wyłapuje się” dziesiątki tysięcy atomów.
By wszystkie miały energię
W praktyce „wyłapuje się” dziesiątki tysięcy atomów.
By wszystkie miały energię
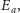 trzeba obniżyć temperaturę do rzędu
mikrokelwinów.
trzeba obniżyć temperaturę do rzędu
mikrokelwinów.
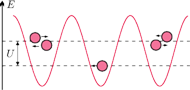
Rys. 4 Sieć optyczna: atomy zimnego gazu (np.
 Rb) znajdują się w okolicach minimów
Rb) znajdują się w okolicach minimów
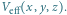 W fizyce klasycznej niemożliwe jest przeskoczenie nad maksimami
W fizyce klasycznej niemożliwe jest przeskoczenie nad maksimami
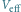 (gdyż energia kinetyczna nie może być ujemna), dozwolone w fizyce kwantowej.
(gdyż energia kinetyczna nie może być ujemna), dozwolone w fizyce kwantowej.
Na zmianę energii atomu można patrzeć, jakby ów znajdował się
w zewnętrznym potencjale
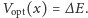 Potencjał ten nie zależy
od czasu – tak naprawdę jest uśrednionym po czasie „efektywnym”
oddziaływaniem z falą stojącą. Tworząc układ trzech prostopadłych laserowych
fal stojących, otrzymamy potencjał
Potencjał ten nie zależy
od czasu – tak naprawdę jest uśrednionym po czasie „efektywnym”
oddziaływaniem z falą stojącą. Tworząc układ trzech prostopadłych laserowych
fal stojących, otrzymamy potencjał

który nazwiemy siecią optyczną.
Jeśli mianownik w równaniu (5) jest dodatni, wówczas potencjał przyjmuje
wartość maksymalną, kiedy amplituda pola elektrycznego jest maksymalna.
Atom jest odpychany od tych obszarów w stronę obszarów, gdzie pole
elektryczne jest stale zerowe – minimów potencjału
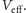 Jeśli
mianownik jest ujemny, wówczas wspomniane obszary zamieniają się rolami
maksimów i minimów.
Jeśli
mianownik jest ujemny, wówczas wspomniane obszary zamieniają się rolami
maksimów i minimów.
Sieć optyczna jako kryształ
Sieć optyczna ma strukturę periodyczną wyznaczoną przez okresowość potencjału efektywnego

można więc układ: sieć optyczna oraz atomy związane potencjałem efektywnym śmiało nazwać kryształem, podobnie jak układ: chmury elektronów i periodycznie ułożonych atomów w kryształach metali.

Rys. 5 Dyslokacja w strukturze krystalicznej metalu. Niedoskonałości w strukturze krystalicznej powodują nieregularności w dynamice elektronów i opór elektryczny.
Badając przewodnictwo (czyli grupowy ruch elektronów) różnych metali,
rozważamy chmurę zdelokalizowanych elektronów poruszających się w całej
objętości kryształu. Kryształy w mikroskali są siecią „żywą”, gdyż atomy
metalu wykonują złożone drgania grupowo, powodując rozchodzenie się fal
zwanych fononami. Niezwykle trudno jest opisać tego typu oddziaływania,
a opisać je trzeba, gdyż możliwa jest zamiana energii elektronów na energię
niesioną przez fonony. Możliwy jest jedynie opis przybliżony. W przypadku
sieci optycznych nie ma fononów – maksima i minima
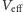 są stałe
w czasie i nie zmieniają położenia. Sieć optyczna jest także idealnie
regularna – nie ma spotykanych w przypadku metali dyslokacji (Rys. 5), czyli
zaburzeń struktury krystalicznej. Dlatego sieć optyczna jest kryształem
idealnym (na tyle, na ile możliwe jest wykonanie idealnie sinusoidalnego
promienia laserowego).
są stałe
w czasie i nie zmieniają położenia. Sieć optyczna jest także idealnie
regularna – nie ma spotykanych w przypadku metali dyslokacji (Rys. 5), czyli
zaburzeń struktury krystalicznej. Dlatego sieć optyczna jest kryształem
idealnym (na tyle, na ile możliwe jest wykonanie idealnie sinusoidalnego
promienia laserowego).
W przypadku konkretnych gazów każdy atom oddziałuje z pozostałymi
atomami w tym samym oczku sieci (i tylko z nimi). Jeśli w oczku znajduje się
 atomów, wówczas mamy tam
atomów, wówczas mamy tam
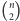 par atomów, z każdą zaś
parą związana jest pewna energia oddziaływania
par atomów, z każdą zaś
parą związana jest pewna energia oddziaływania
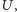 przy czym
przy czym
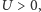 jeśli atomy odpychają się, a
jeśli atomy odpychają się, a
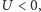 jeśli się przyciągają.
Energia
jeśli się przyciągają.
Energia
 zależy od budowy wewnętrznej atomów. Co ciekawe,
można manipulować wielkością
zależy od budowy wewnętrznej atomów. Co ciekawe,
można manipulować wielkością
 oświetlając gaz dodatkowym
laserem o odpowiednio dobranej częstotliwości oraz teoretycznie można
ustalić
oświetlając gaz dodatkowym
laserem o odpowiednio dobranej częstotliwości oraz teoretycznie można
ustalić
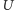 równe dowolnej liczbie rzeczywistej. Wykorzystywane jest
zjawisko tzw. rezonansu Feshbacha.
równe dowolnej liczbie rzeczywistej. Wykorzystywane jest
zjawisko tzw. rezonansu Feshbacha.
Rys. 6 Cała sieć będzie składać się z kilku obszarów – w każdym z osobna
 będzie
wielokrotnością
będzie
wielokrotnością
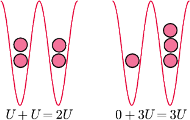
Rys. 7 Minimalny koszt przeskoku atomu to
 W przypadku klasycznego
przewodnictwa można by powiedzieć, że pasmo przewodnictwa znajduje się w odległości
W przypadku klasycznego
przewodnictwa można by powiedzieć, że pasmo przewodnictwa znajduje się w odległości
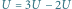 od pasma „walencyjnego”.
od pasma „walencyjnego”.
Rozpatrzmy fragment sieci optycznej, składający się z
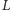 oczek sieci
i zawierający
oczek sieci
i zawierający
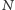 atomów. Załóżmy, że
atomów. Załóżmy, że
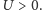 Jeśli
Jeśli
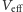 ma wysoką amplitudę, wówczas tunelowanie (przeskakiwanie między
oczkami sieci) nie jest łatwe, a w każdym oczku sieci znajduje się ustalona
liczba atomów. Całkowita energia będzie minimalna, gdy oczka sieci
będą równo obsadzone. Zakładamy, że
ma wysoką amplitudę, wówczas tunelowanie (przeskakiwanie między
oczkami sieci) nie jest łatwe, a w każdym oczku sieci znajduje się ustalona
liczba atomów. Całkowita energia będzie minimalna, gdy oczka sieci
będą równo obsadzone. Zakładamy, że
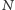 jest wielokrotnością
jest wielokrotnością
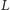 (Rys. 6). W opisanej sytuacji układ zachowuje się jak izolator –
przeskakiwanie atomów jest energetycznie kosztowne. Jeśli w dwóch oczkach
znajdują się po dwa atomy, wówczas energia odpychania się atomów jest
równa
(Rys. 6). W opisanej sytuacji układ zachowuje się jak izolator –
przeskakiwanie atomów jest energetycznie kosztowne. Jeśli w dwóch oczkach
znajdują się po dwa atomy, wówczas energia odpychania się atomów jest
równa
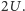 Gdyby jeden z tych atomów przeskoczył do drugiego oczka,
wówczas całkowita energia wyniosłaby
Gdyby jeden z tych atomów przeskoczył do drugiego oczka,
wówczas całkowita energia wyniosłaby
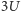 (Rys. 7) i układ jest
izolatorem. Jest to inny mechanizm powstawania izolatora: tunelowanie jako takie
było możliwe (czyli układ powinien być przewodnikiem), ale energetycznie
kosztowne (koszt:
(Rys. 7) i układ jest
izolatorem. Jest to inny mechanizm powstawania izolatora: tunelowanie jako takie
było możliwe (czyli układ powinien być przewodnikiem), ale energetycznie
kosztowne (koszt:
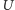 na cząstkę). Wzajemne odpychanie się atomów
zdominowało ewentualne tunelowanie i układ okazał się izolatorem. Taki układ
nazywamy izolatorem Motta.
na cząstkę). Wzajemne odpychanie się atomów
zdominowało ewentualne tunelowanie i układ okazał się izolatorem. Taki układ
nazywamy izolatorem Motta.
Sieci optyczne są nowym materiałem, będącym cały czas przedmiotem aktywnych badań. W ostatnich latach bardzo szybko pojawiają się nowe możliwości eksperymentalne, rozwijana jest teoria. Można je zastosować do badania mechanizmów fizyki ciała stałego. Niedawno pojawiły się też możliwości symulowania oddziaływań znanych do tej pory z fizyki wysokich energii. W sierpniu 2010 ogłoszono sukces w manipulowaniu pojedynczymi oczkami sieci optycznej. Być może w niedalekiej przyszłości każde oczko sieci będzie mogło być kubitem w komputerze kwantowym opartym na sieci optycznej.
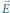 fali stojącej dla różnych
fali stojącej dla różnych
 (dla
(dla
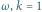 ). Jeśli mianownik w równaniu (5) jest dodatni, to
). Jeśli mianownik w równaniu (5) jest dodatni, to
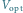 jest postaci (a),
jest natomiast postaci (b), jeśli jest ujemny.
jest postaci (a),
jest natomiast postaci (b), jeśli jest ujemny.
 Rb) znajdują się w okolicach minimów
Rb) znajdują się w okolicach minimów
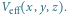 W fizyce klasycznej niemożliwe jest przeskoczenie nad maksimami
W fizyce klasycznej niemożliwe jest przeskoczenie nad maksimami
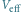 (gdyż energia kinetyczna nie może być ujemna), dozwolone w fizyce kwantowej.
(gdyż energia kinetyczna nie może być ujemna), dozwolone w fizyce kwantowej.
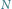 będzie
wielokrotnością
będzie
wielokrotnością
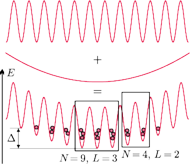
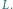 W praktyce sieci znajdują się w pułapce – zewnętrzny potencjał
sprawia, że skończona liczba oczek jest obsadzana –
W praktyce sieci znajdują się w pułapce – zewnętrzny potencjał
sprawia, że skończona liczba oczek jest obsadzana –
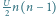 jest mniejsze niż
różnica między energiami na dnie oczek –
jest mniejsze niż
różnica między energiami na dnie oczek –
 na rysunku.
na rysunku.
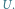 W przypadku klasycznego
przewodnictwa można by powiedzieć, że pasmo przewodnictwa znajduje się w odległości
W przypadku klasycznego
przewodnictwa można by powiedzieć, że pasmo przewodnictwa znajduje się w odległości
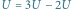 od pasma „walencyjnego”.
od pasma „walencyjnego”.
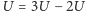 od pasma
„walencyjnego”.
od pasma
„walencyjnego”.