Klub 44F - zadania IX 2011»Zadanie 522
o zadaniu...
- Zadanie pochodzi z artykułu Klub 44F - zadania IX 2011
- Publikacja w Delcie: wrzesień 2011
- Publikacja elektroniczna: 31 sierpnia 2011
- Artykuł źródłowy w wersji do druku [application/pdf]: (81 KB)
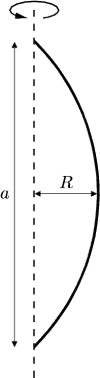
Linka o długości
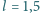 m i masie
m i masie
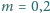 kg (jednorodnie
rozłożonej) jest zamocowana końcami w dwóch punktach odległych o
kg (jednorodnie
rozłożonej) jest zamocowana końcami w dwóch punktach odległych o
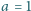 m (Rys. 1). Linka obraca się wokół osi przechodzącej przez punkty
zamocowania z prędkością kątową
m (Rys. 1). Linka obraca się wokół osi przechodzącej przez punkty
zamocowania z prędkością kątową
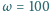 rad/s i względem tego
obracającego się układu odniesienia pozostaje nieruchoma. Pomijając efekty siły
ciężkości, obliczyć numerycznie odległość
rad/s i względem tego
obracającego się układu odniesienia pozostaje nieruchoma. Pomijając efekty siły
ciężkości, obliczyć numerycznie odległość
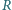 środkowego punktu
linki od osi obrotu.
środkowego punktu
linki od osi obrotu.

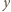 będzie współrzędną wzdłuż osi obrotu, natomiast
będzie współrzędną wzdłuż osi obrotu, natomiast
 – współrzędną wzdłuż osi prostopadłej. Składowa
– współrzędną wzdłuż osi prostopadłej. Składowa
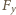 siły
napięcia linki jest stała, natomiast przyrost składowej
siły
napięcia linki jest stała, natomiast przyrost składowej
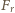 równoważy siłę
odśrodkową działającą na fragment linki o długości
równoważy siłę
odśrodkową działającą na fragment linki o długości
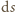 i masie
i masie
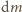 :
:
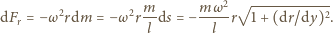
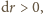
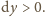 Kierunek
siły napięcia jest styczny do linki, czyli
Kierunek
siły napięcia jest styczny do linki, czyli
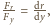 a stąd
a stąd
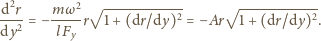
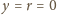 i dowolnie
wybranych wartości
i dowolnie
wybranych wartości
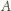 oraz
oraz
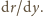 Wartości te należy dobrać
tak, aby w punkcie
Wartości te należy dobrać
tak, aby w punkcie
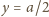 osiągnąć
osiągnąć
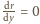 oraz długość linki
równą
oraz długość linki
równą
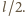 Okazuje się, że przy danych
Okazuje się, że przy danych
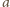 i
i
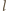 właściwymi
wyborami są
właściwymi
wyborami są
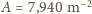 (faktycznie wyznaczamy w ten sposób
(faktycznie wyznaczamy w ten sposób
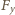 ; wartości
; wartości
 i
i
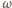 nie wpływają na kształt linki) oraz
nie wpływają na kształt linki) oraz
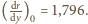 Maksymalną wartością
Maksymalną wartością
 jest
jest
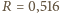 m.
Dla porównania, dla krzywej łańcuchowej (cosinusa hiperbolicznego) byłoby
m.
Dla porównania, dla krzywej łańcuchowej (cosinusa hiperbolicznego) byłoby