Aktualności (nie tylko) fizyczne
Nowe pomysły
Nadprzewodzący półtorak
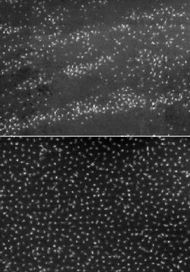
Paterny worteksów magnetycznych w diborku magnezu
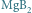 – nowo odkrytym
nadprzewodniku typu 1,5 (góra) oraz w diselenku niobu
– nowo odkrytym
nadprzewodniku typu 1,5 (góra) oraz w diselenku niobu
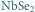 – nadprzewodniku
typu 2 (dół).
– nadprzewodniku
typu 2 (dół).
Dzięki pracom Lwa Landaua i Witalija Ginzburga od połowy ubiegłego wieku
wiadomo, że możliwe są dwa typy nadprzewodników. Pierwszy wykazuje
efekt Meissnera: jest doskonałym diamagnetykiem. W zewnętrznym, niezbyt
silnym polu magnetycznym wzbudzane są w takim nadprzewodniku
prądy wirowe, które doskonale kompensują pole w jego wnętrzu. Pole
magnetyczne nie wnika więc do takiego nadprzewodnika. Gdy jest zbyt silne, to
nadprzewodnik przestaje nim być. Wszystkie nadprzewodniki znane w czasach,
kiedy prace Landaua i Ginzburga powstawały, były właśnie tego typu.
Zauważyli oni jednak, że gdyby pewien parametr
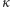 , nazywany obecnie
parametrem GL, mógł, dla jakiegoś nadprzewodnika, przyjąć wartość
większą od
, nazywany obecnie
parametrem GL, mógł, dla jakiegoś nadprzewodnika, przyjąć wartość
większą od
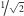 , to nadprzewodnik taki mógłby wpuścić do swego
wnętrza pole magnetyczne, nie przestając być nadprzewodnikiem. Parametr ten
jest stosunkiem głębokości powierzchniowej penetracji nadprzewodnika przez
pole magnetyczne do długości koherencji, wielkości charakteryzującej
przestrzenne uporządkowanie funkcji falowej opisującej stan nadprzewodnictwa.
Przy ogrzewaniu nadprzewodnika do temperatury krytycznej obydwa te
parametry rosną nieograniczenie, ale ich stosunek pozostaje stały dla danego
materiału nadprzewodzącego.
, to nadprzewodnik taki mógłby wpuścić do swego
wnętrza pole magnetyczne, nie przestając być nadprzewodnikiem. Parametr ten
jest stosunkiem głębokości powierzchniowej penetracji nadprzewodnika przez
pole magnetyczne do długości koherencji, wielkości charakteryzującej
przestrzenne uporządkowanie funkcji falowej opisującej stan nadprzewodnictwa.
Przy ogrzewaniu nadprzewodnika do temperatury krytycznej obydwa te
parametry rosną nieograniczenie, ale ich stosunek pozostaje stały dla danego
materiału nadprzewodzącego.
Uczeń Landaua, Aleksiej Abrikosow, wykazał, że drugi typ nadprzewodnictwa
wiąże się z powstawaniem ,,wirów” zawierających pojedynczy kwant
strumienia indukcji magnetycznej
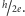 W nadprzewodniku pierwszego
typu takie worteksy też mogłyby powstać, ale dla
W nadprzewodniku pierwszego
typu takie worteksy też mogłyby powstać, ale dla
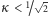 przyciągają się
i w efekcie zlewają się, powodując wyjście ze stanu nadprzewodnictwa,
natomiast dla
przyciągają się
i w efekcie zlewają się, powodując wyjście ze stanu nadprzewodnictwa,
natomiast dla
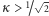 odpychają się i w efekcie tworzą regularną sieć,
a nadprzewodzenie kończy się dopiero wtedy, gdy pole magnetyczne jest na tyle
silne, że te wiry zaczynają się przekrywać.
odpychają się i w efekcie tworzą regularną sieć,
a nadprzewodzenie kończy się dopiero wtedy, gdy pole magnetyczne jest na tyle
silne, że te wiry zaczynają się przekrywać.
Zjawisko nadprzewodnictwa jest rodzajem kondensacji Bosego–Einsteina. Kondensacja taka jest możliwa tylko dla obiektów (zwanych bozonami), które ,,lubią” znajdować się wszystkie w tym samym stanie – w odróżnieniu od fermionów, z których żadne dwa nie mogą znajdować się w tym samym stanie (podlegają zakazowi Pauliego). Bozonami są np. fotony i to właśnie umożliwia akcję laserową, a fermionami są np. elektrony i dzięki temu mogą istnieć stabilne atomy różniące się własnościami chemicznymi, a nie jedynie masą.
O tym, czy dany obiekt jest fermionem czy bozonem, decyduje jego spin,
czyli wewnętrzny moment pędu. Bozony mają spin całkowity, a fermiony
połówkowy. Nadprzewodnictwo jest możliwe dzięki temu, że elektrony
w niskiej temperaturze łączą się w pary, które mają sumaryczny spin całkowity,
a więc są bozonami. Elektrony tworzące takie pary pochodzą zawsze z pasma
przewodnictwa. Okazuje się, że istnieją materiały, takie jak diborek magnezu
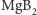 , w których w zjawisku nadprzewodnictwa uczestniczą elektrony
z dwóch pasm przewodnictwa. Materiał taki charakteryzuje się dwoma
parametrami uporządkowania, i to w dodatku na tyle różnymi, że
odpowiadałyby one albo jednemu, albo drugiemu typowi nadprzewodnictwa.
Okazało się, że odpowiadają obydwu. Pod wpływem zewnętrznego pola
magnetycznego powstają w diborku magnezu worteksy, które wykazują
krótkozasięgowe odpychanie, ale długozasięgowe przyciąganie. W rezultacie
tworzą się w tym materiale agregaty albo pasma wirów, zamiast regularnej
sieci [1]. Tym samym odkryto nowy rodzaj nadprzewodnika, który jako
pośredni między typami jeden i dwa został nazwany typem jeden i pół.
Otwiera się w ten sposób zupełnie nowy obszar badań oraz, prawdopodobnie,
ciekawych zastosowań.
, w których w zjawisku nadprzewodnictwa uczestniczą elektrony
z dwóch pasm przewodnictwa. Materiał taki charakteryzuje się dwoma
parametrami uporządkowania, i to w dodatku na tyle różnymi, że
odpowiadałyby one albo jednemu, albo drugiemu typowi nadprzewodnictwa.
Okazało się, że odpowiadają obydwu. Pod wpływem zewnętrznego pola
magnetycznego powstają w diborku magnezu worteksy, które wykazują
krótkozasięgowe odpychanie, ale długozasięgowe przyciąganie. W rezultacie
tworzą się w tym materiale agregaty albo pasma wirów, zamiast regularnej
sieci [1]. Tym samym odkryto nowy rodzaj nadprzewodnika, który jako
pośredni między typami jeden i dwa został nazwany typem jeden i pół.
Otwiera się w ten sposób zupełnie nowy obszar badań oraz, prawdopodobnie,
ciekawych zastosowań.
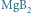 – nowo odkrytym
nadprzewodniku typu 1,5 (góra) oraz w diselenku niobu
– nowo odkrytym
nadprzewodniku typu 1,5 (góra) oraz w diselenku niobu
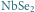 – nadprzewodniku
typu 2 (dół).
– nadprzewodniku
typu 2 (dół).