Co to jest?
Masa relatywistyczna
Jedną z konsekwencji teorii względności Einsteina jest wzrost bezwładności ciał w ruchu. W skrócie, im szybciej porusza się ciało, tym trudniej jest zmienić jego prędkość. Ponieważ wielkością będącą miarą bezwładności w fizyce jest masa, kuszącym pomysłem jest, aby tłumaczyć ten efekt wzrostem masy właśnie. Wiele materiałów dotyczących Szczególnej Teorii Względności wprowadza wobec tego podział na "masę spoczynkową", czyli masę, którą ciało ma w bezruchu, i "masę relatywistyczną", czyli masę ciała w ruchu, większą od spoczynkowej...

Tradycyjnie masę spoczynkową oznacza się wtedy 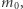 a masa relatywistyczna
a masa relatywistyczna 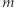 wyraża się wzorem:
wyraża się wzorem:
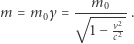 |
Wprowadzenie tych pojęć ma pewne przyjemne konsekwencje dla estetyki równań teorii względności. Na przykład energia wyraża się wtedy słynnym wzorem Einsteina 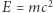 niezależnie od prędkości ciała, a pęd dany jest przez znane z fizyki klasycznej
niezależnie od prędkości ciała, a pęd dany jest przez znane z fizyki klasycznej 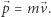 Wydaje się więc, że mogą one być całkiem użyteczne.
Wydaje się więc, że mogą one być całkiem użyteczne.
Wśród fizyków kwestia użyteczności masy relatywistycznej okazuje się jednak co najmniej dyskusyjna. Istnieje ku temu kilka powodów, z których przedstawię trzy.
Wzrost bezwładności
Jak już wspomniałem, zgodnie z teorią względności bezwładność ciał rośnie wraz ze wzrostem ich prędkości. Okazuje się jednak, że opis tego zjawiska jako wzrost masy powoduje trochę niewidocznych na pierwszy rzut oka trudności. W czym problem?
Zacznijmy od szybkiego przypomnienia fizyki przedrelatywistycznej. Zgodnie z II zasadą dynamiki Newtona, jeśli na ciało działa siła 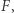 to ciało porusza się z przyspieszeniem
to ciało porusza się z przyspieszeniem 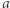 proporcjonalnym do tej siły, a współczynnik proporcjonalności to właśnie masa. Konkretnie,
proporcjonalnym do tej siły, a współczynnik proporcjonalności to właśnie masa. Konkretnie, 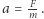
Co więcej, ciało zawsze przyspiesza w tym kierunku, w którym działa siła (co może wydawać się oczywiste..., ale nie uprzedzajmy faktów). Można wobec tego związek powyżej zapisać wektorowo: 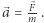
Co w tym opisie zmienia teoria względności?
Jeśli zostaniemy przy podziale na masę spoczynkową i relatywistyczną, powiemy, że ciało w spoczynku ma masę 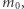 a w ruchu masę
a w ruchu masę 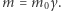 Na intuicję, chciałoby się napisać, że w takim razie w przypadku relatywistycznym przyspieszenie będzie wyrażać się wzorem
Na intuicję, chciałoby się napisać, że w takim razie w przypadku relatywistycznym przyspieszenie będzie wyrażać się wzorem 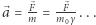 Ale czy tak jest rzeczywiście?
Ale czy tak jest rzeczywiście?
Cóż... prawie. Ten wzór ma zastosowanie, ale pod jednym warunkiem - że siła 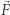 jest prostopadła do prędkości
jest prostopadła do prędkości 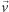 ciała. Gdy siła i prędkość są równoległe, okazuje się, że przyspieszenie wynosi
ciała. Gdy siła i prędkość są równoległe, okazuje się, że przyspieszenie wynosi 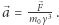
Jedną z ciekawych konsekwencji tego stanu rzeczy jest coś, co zasugerowałem już wcześniej - otóż siła nie musi być zawsze równoległa do przyspieszenia. Wobec tego nie istnieje wielkość skalarna, którą moglibyśmy zastosować w miejscu masy w II zasadzie dynamiki. Jeśli chcemy zachować wzór Newtona, masa w tym wzorze musi być tensorem drugiego rzędu (który można zapisać jako macierz). Samo wprowadzenie masy relatywistycznej nie rozwiązuje więc problemu rosnącej bezwładności.
Zderzenia
Jednym ze sposobów porównywania mas ciał może być zderzanie ich ze sobą. Jeśli masywniejsze ciało A uderza w spoczywające, mniej masywne ciało B, to ciało A lekko zwalnia, a ciało B jest odbijane ze sporą prędkością. I odwrotnie - jeśli to mniej masywne ciało C uderza w masywniejsze ciało D, to ciało C się odbija, a ciało D uzyskuje tylko niewielką prędkość.
W szczególnym przypadku, kiedy ciała zderzające się mają równe masy, to pierwsze ciało się zatrzyma, a drugie zacznie poruszać się z taką prędkością, jaką miało pierwsze ciało przed zderzeniem (przynajmniej w przypadku zderzenia idealnie sprężystego). Jedną z bardziej znanych ilustracji tego zjawiska jest tzw. kołyska Newtona.
Pytanie jest wobec tego takie - jak zachowają się ciała, które mają identyczną masę spoczynkową, ale różną relatywistyczną? Na przykład, co jeśli kulka o masie spoczynkowej 1 grama, rozpędzona do 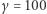 (czyli jej masa relatywistyczna to 100 gramów) uderzy w drugą identyczną, spoczywającą?
(czyli jej masa relatywistyczna to 100 gramów) uderzy w drugą identyczną, spoczywającą?
Odpowiedź można znaleźć na podstawie zasad zachowania energii i pędu. Tu nie będziemy tego robić - szczegółowe obliczenia pozostawię Czytelnikowi. Podam jedynie wynik.
Otóż okazuje się, że kulki w tej sytuacji zachowają się jak ciała o równych masach. To znaczy - kulka poruszająca się po uderzeniu zatrzyma się, a kulka spoczywająca ruszy z taką samą prędkością, jaką miała pierwsza przed uderzeniem. Masa relatywistyczna okazuje się nie mieć tu żadnego znaczenia. Poprawną odpowiedź daje rozważenie wyłącznie mas spoczynkowych.
Duplikowanie pojęć
Ten powód jest mniej fizyczny, a bardziej techniczno-estetyczny, ale również ma pewną wagę.
Fizycy lubią upraszczać sobie życie. Jednym ze środków do osiągnięcia tego celu jest eliminowanie stałych przyrody z równań. Już wyjaśniam.
Weźmy za przykład prędkość światła w próżni. W tablicach fizycznych odczytujemy, że wynosi ona 299 792 458 m/s. Niezbyt ładna liczba, ale nie mamy wpływu na to, jak natura dobrała sobie prędkość fal elektromagnetycznych... Czy może mamy?
Ta konkretna liczba wynika tylko z doboru jednostek. Gdybyśmy chcieli wyrazić prędkość światła np. w stopach na tydzień, liczba byłaby inna. Gdybyśmy mierzyli w łokciach na rok - jeszcze inna. Przez odpowiedni dobór jednostek można sprawić, że wartość liczbowa prędkości światła może być całkowicie dowolna. W szczególności, można wybrać jednostki, w których prędkość światła wynosi... po prostu 1.
Fizycy bardzo lubią korzystać z tej możliwości. Przykładowe jednostki, które dają taką wartość 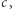 to sekunda i sekunda świetlna. Inne to rok i rok świetlny. Albo jakakolwiek jednostka czasu i odległość, jaką światło przebywa w ciągu tej jednostki. Dowolny taki wybór sprawia, że
to sekunda i sekunda świetlna. Inne to rok i rok świetlny. Albo jakakolwiek jednostka czasu i odległość, jaką światło przebywa w ciągu tej jednostki. Dowolny taki wybór sprawia, że 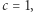 i jak za dotknięciem magicznej różdżki,
i jak za dotknięciem magicznej różdżki,  znika ze wszystkich równań, bo czy mnożymy przez 1, czy dzielimy - nic się w równaniu nie zmienia.
znika ze wszystkich równań, bo czy mnożymy przez 1, czy dzielimy - nic się w równaniu nie zmienia.
(Fizycy lubią iść jeszcze dalej i pozbywać się kolejnych stałych. Często spotykanym wyborem są jednostki, w których 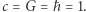 Te jednostki są zwane jednostkami naturalnymi albo jednostkami Plancka - podstawowymi jednostkami w tym układzie są długość Plancka, czas Plancka i masa Plancka.)
Te jednostki są zwane jednostkami naturalnymi albo jednostkami Plancka - podstawowymi jednostkami w tym układzie są długość Plancka, czas Plancka i masa Plancka.)
Jakie to wszystko ma znaczenie? Zobaczmy, co w tym kontekście dzieje się ze słynnym wzorem Einsteina na energię:
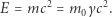 |
Gdy wprowadzimy jednostki takie, że 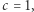 dostajemy:
dostajemy:
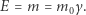 |
W takich jednostkach masa relatywistyczna jest po prostu równa energii! Wobec tego jest de facto duplikatem pojęcia energii. Wszędzie tam, gdzie korzystalibyśmy z masy relatywistycznej, można wstawić energię (lub 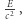 jeśli
jeśli 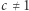 ) i równania będą poprawne bez dokładania nowego pojęcia.
) i równania będą poprawne bez dokładania nowego pojęcia.
Podsumowanie
Jak widać, pozorna użyteczność masy relatywistycznej mocno maleje przy bliższym spojrzeniu na sprawę. Pojęcie to nie sprawdza się jako miara bezwładności, nie pomaga w rozważaniu zderzeń oraz może być zastąpione energią. Z tych powodów fizycy raczej już tego pojęcia nie stosują - kiedy fizyk mówi o masie, praktycznie zawsze ma na myśli masę spoczynkową.
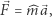
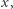 można rozpisać jako:
można rozpisać jako: