Zadanie ZF-951
o zadaniu...
- Publikacja w Delcie: maj 2018
- Publikacja elektroniczna: 30 kwietnia 2018
Energia wiązania cząsteczki tlenu 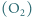 wynosi
wynosi 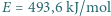 . Jaka jest minimalna wartość prędkości cząsteczek tlenu, dla której ich zderzenia niesprężyste mogą doprowadzić do zerwania wiązania przynajmniej jednej z nich? Jakiej temperaturze gazu odpowiada ta prędkość? Stała Boltzmanna
. Jaka jest minimalna wartość prędkości cząsteczek tlenu, dla której ich zderzenia niesprężyste mogą doprowadzić do zerwania wiązania przynajmniej jednej z nich? Jakiej temperaturze gazu odpowiada ta prędkość? Stała Boltzmanna 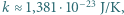 liczba Avogadro
liczba Avogadro 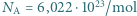 , masa tlenu wynosi
, masa tlenu wynosi 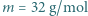 .
.
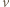 spełnia więc warunek:
spełnia więc warunek: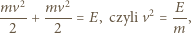
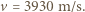
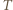 wynosi
wynosi 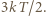 Otrzymanej prędkości
Otrzymanej prędkości  odpowiada więc temperatura:
odpowiada więc temperatura: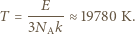
 21% tlenu
21% tlenu 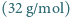 i 1% argonu
i 1% argonu 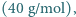 znaleźć prawdopodobieństwo fluktuacji gęstości tych gazów na poziomie większym niż 1% (dla objętości rozpatrywanych w przykładzie zilustrowanym tabelką w poniższej uwadze).
znaleźć prawdopodobieństwo fluktuacji gęstości tych gazów na poziomie większym niż 1% (dla objętości rozpatrywanych w przykładzie zilustrowanym tabelką w poniższej uwadze).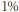 zależy bardzo silnie od promienia
zależy bardzo silnie od promienia  kuli, co widać z przytoczonej tabelki:
kuli, co widać z przytoczonej tabelki:![|-------|------|-------|-------|--------|-------| |r-[cm]--|--1---|5⋅10−5-|3⋅10−5-|2,5-⋅10−5|1-⋅10−5-| |θ [sek] |101014 | 1068 | 106 | 1 | 10−11 | -------------------------------------------------](/math/temat/fizyka/fizyka_statystyczna/zadania/2017/08/19/zf-466/3x-cee258ad6f163cb2712edf33b3db7796fca90dc8-dm-66,57,43-FF,FF,FF.gif)
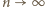 rozkład Poissona przechodzi na rozkład Gaussa (można to sprawdzić korzystając najpierw ze wzoru Stirlinga, a następnie z rozwinięcia logarytmu w szereg z dokładnością do dwóch wyrazów), mamy
rozkład Poissona przechodzi na rozkład Gaussa (można to sprawdzić korzystając najpierw ze wzoru Stirlinga, a następnie z rozwinięcia logarytmu w szereg z dokładnością do dwóch wyrazów), mamy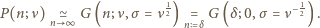
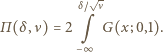
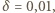 pozostaje więc tylko obliczenie
pozostaje więc tylko obliczenie 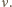 W tym celu obliczamy liczbę molekuł gazu w najmniejszej z rozpatrywanych objętości
W tym celu obliczamy liczbę molekuł gazu w najmniejszej z rozpatrywanych objętości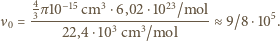


 oznacza średnią liczbę cząsteczek w małej objętości
oznacza średnią liczbę cząsteczek w małej objętości 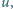 a
a 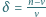 nazywane jest zagęszczeniem liczby cząsteczek w objętości
nazywane jest zagęszczeniem liczby cząsteczek w objętości 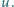 (Zakładamy, że w naczyniu o objętości
(Zakładamy, że w naczyniu o objętości 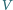 znajduje się
znajduje się  cząsteczek.)
cząsteczek.)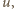 będącej częścią dużo większej objętości
będącej częścią dużo większej objętości 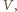 jest proporcjonalne do
jest proporcjonalne do 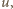 otrzymujemy, że liczba cząsteczek w objętości
otrzymujemy, że liczba cząsteczek w objętości  podlega statystyce Poissona
podlega statystyce Poissona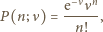
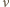 jest średnią liczbą cząsteczek w objętości
jest średnią liczbą cząsteczek w objętości 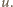 Wiedząc, że wariancja rozkładu Poissona
Wiedząc, że wariancja rozkładu Poissona 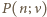 wynosi
wynosi 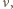 dostajemy
dostajemy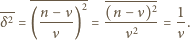
 dolny koniec jest zamknięty,
a górny otwarty. W dolnej połowie znajduje się gaz doskonały o temperaturze
dolny koniec jest zamknięty,
a górny otwarty. W dolnej połowie znajduje się gaz doskonały o temperaturze
 górna połowa jest wypełniona rtęcią. Ciśnienie zewnętrzne
jest równe ciśnieniu słupka rtęci o wysokości
górna połowa jest wypełniona rtęcią. Ciśnienie zewnętrzne
jest równe ciśnieniu słupka rtęci o wysokości
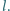 Do jakiej
temperatury wystarczy ogrzać gaz w rurce, aby cała rtęć została z niej
wyparta?
Do jakiej
temperatury wystarczy ogrzać gaz w rurce, aby cała rtęć została z niej
wyparta?
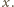 Temperaturę gazu
Temperaturę gazu
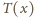 możemy otrzymać
z równania Clapeyrona:
możemy otrzymać
z równania Clapeyrona:
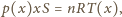
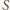 jest powierzchnią przekroju rurki, a warunek równowagi
ciśnień ma postać
jest powierzchnią przekroju rurki, a warunek równowagi
ciśnień ma postać
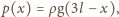
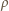 jest gęstością rtęci. Temperatura jest kwadratową
funkcją
jest gęstością rtęci. Temperatura jest kwadratową
funkcją
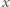 :
:
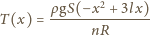
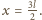 Temperatura
Temperatura
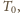 do której wystarczy
ogrzać gaz w rurce, wynosi więc
do której wystarczy
ogrzać gaz w rurce, wynosi więc
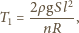
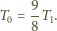
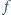 dźwięku piszczałki wypełnionej
helem, jeśli wypełniona powietrzem generuje dźwięk o częstotliwości
dźwięku piszczałki wypełnionej
helem, jeśli wypełniona powietrzem generuje dźwięk o częstotliwości
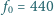 Hz? Prędkość
Hz? Prędkość
 dźwięku w gazie, w warunkach
normalnych, z dobrym przybliżeniem opisuje zależność
dźwięku w gazie, w warunkach
normalnych, z dobrym przybliżeniem opisuje zależność

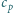 i
i
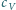 oznaczają odpowiednio ciepła właściwe gazu pod
stałym ciśnieniem i w stałej objętości,
oznaczają odpowiednio ciepła właściwe gazu pod
stałym ciśnieniem i w stałej objętości,
 –
temperaturę w skali Kelvina, a
–
temperaturę w skali Kelvina, a
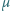 – masę jednego mola gazu. Powietrze jest
mieszaniną azotu (78% objętości) i tlenu (21% objętości).
– masę jednego mola gazu. Powietrze jest
mieszaniną azotu (78% objętości) i tlenu (21% objętości).
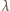 fali generowanego dźwięku jest proporcjonalna do
długości
fali generowanego dźwięku jest proporcjonalna do
długości
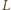 piszczałki (współczynnik zależy od rodzaju piszczałki i nie
zależy od rodzaju wypełniającego ją gazu), z definicji:
piszczałki (współczynnik zależy od rodzaju piszczałki i nie
zależy od rodzaju wypełniającego ją gazu), z definicji:
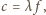 a więc
częstotliwość
a więc
częstotliwość
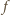 dźwięku danej piszczałki jest proporcjonalna do
prędkości dźwięku w wypełniającym ją gazie. Powietrze to w ponad
dźwięku danej piszczałki jest proporcjonalna do
prędkości dźwięku w wypełniającym ją gazie. Powietrze to w ponad
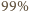 mieszanina dwuatomowych cząsteczek azotu
mieszanina dwuatomowych cząsteczek azotu
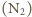 i tlenu
i tlenu
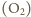 o wypadkowej masie molowej
o wypadkowej masie molowej
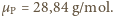 Cząsteczki
helu, gazu szlachetnego, są jednoatomowe:
Cząsteczki
helu, gazu szlachetnego, są jednoatomowe:
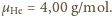 Jak
wiadomo, stosunek
Jak
wiadomo, stosunek
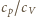 dla gazu jednoatomowego wynosi
w przybliżeniu 5/3, a dla gazu dwuatomowego 7/5. Po podstawieniu tych
danych otrzymujemy
dla gazu jednoatomowego wynosi
w przybliżeniu 5/3, a dla gazu dwuatomowego 7/5. Po podstawieniu tych
danych otrzymujemy
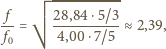
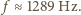
 Naczynie to oddzielone jest od pustego naczynia o objętości
Naczynie to oddzielone jest od pustego naczynia o objętości
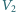 przegrodą, która przepuszcza wodór, natomiast nie przepuszcza
helu. Po ustaleniu się równowagi ciśnienie w pierwszym naczyniu
zmalało dwukrotnie. Jaki jest stosunek
przegrodą, która przepuszcza wodór, natomiast nie przepuszcza
helu. Po ustaleniu się równowagi ciśnienie w pierwszym naczyniu
zmalało dwukrotnie. Jaki jest stosunek
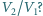 Temperatura jest
stała.
Temperatura jest
stała.
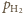 i
i
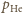 ciśnienia cząstkowe wodoru i helu
w chwili początkowej, przez
ciśnienia cząstkowe wodoru i helu
w chwili początkowej, przez
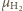 i
i
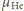 ich masy molowe,
a jednakowe masy obu gazów przez
ich masy molowe,
a jednakowe masy obu gazów przez
 Z równań Clapeyrona wynika,
że stosunek ciśnień cząstkowych wynosi
Z równań Clapeyrona wynika,
że stosunek ciśnień cząstkowych wynosi
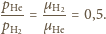
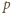 jest sumą ciśnień cząstkowych:
jest sumą ciśnień cząstkowych:
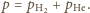 Stan równowagi nastąpi, gdy liczba cząsteczek wodoru
w jednostce objętości po obu stronach przegrody będzie taka sama, a tym
samym jednakowe będą ciśnienia wodoru
Stan równowagi nastąpi, gdy liczba cząsteczek wodoru
w jednostce objętości po obu stronach przegrody będzie taka sama, a tym
samym jednakowe będą ciśnienia wodoru
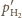 w obu naczyniach.
Oznaczając przez
w obu naczyniach.
Oznaczając przez
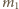 i
i
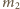 masy wodoru w pierwszym i drugim
naczyniu w stanie końcowym
masy wodoru w pierwszym i drugim
naczyniu w stanie końcowym
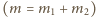 , z równań Clapeyrona
otrzymujemy:
, z równań Clapeyrona
otrzymujemy:
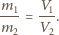
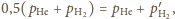 stąd
(uwzględniając, że
stąd
(uwzględniając, że
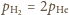 ) mamy
) mamy
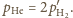 Korzystając
ponownie z równań Clapeyrona dla helu w pierwszym naczyniu i wodoru
w drugim, otrzymujemy
Korzystając
ponownie z równań Clapeyrona dla helu w pierwszym naczyniu i wodoru
w drugim, otrzymujemy
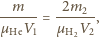
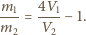
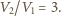
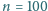 moli gazu doskonałego o temperaturze
moli gazu doskonałego o temperaturze
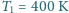 i pod ciśnieniem
i pod ciśnieniem
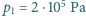 znajduje się
w otoczeniu powietrza atmosferycznego o temperaturze
znajduje się
w otoczeniu powietrza atmosferycznego o temperaturze
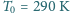 i pod
ciśnieniem
i pod
ciśnieniem
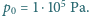 Obliczyć maksymalną pracę, którą może
wykonać zespół gaz + otoczenie (zarówno bezpośrednio, jak za
pośrednictwem maszyn cieplnych). Ciepło molowe gazu przy stałej objętości
jest równe
Obliczyć maksymalną pracę, którą może
wykonać zespół gaz + otoczenie (zarówno bezpośrednio, jak za
pośrednictwem maszyn cieplnych). Ciepło molowe gazu przy stałej objętości
jest równe
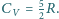
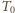 i ciśnienia
i ciśnienia
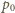 w procesie odwracalnym. Na przykład, można
najpierw rozprężyć gaz adiabatycznie do temperatury
w procesie odwracalnym. Na przykład, można
najpierw rozprężyć gaz adiabatycznie do temperatury
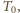 a następnie
dokonać sprężenia lub rozprężenia izotermicznego, aby osiągnąć ciśnienie
a następnie
dokonać sprężenia lub rozprężenia izotermicznego, aby osiągnąć ciśnienie
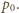 Pomijając na razie pracę powietrza atmosferycznego, pracę przy
rozprężeniu adiabatycznym
Pomijając na razie pracę powietrza atmosferycznego, pracę przy
rozprężeniu adiabatycznym
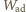 znajdziemy jako różnicę początkowej
i końcowej energii wewnętrznej:
znajdziemy jako różnicę początkowej
i końcowej energii wewnętrznej:
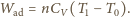
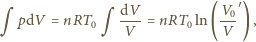
 jest objętością gazu po rozprężeniu adiabatycznym, a
jest objętością gazu po rozprężeniu adiabatycznym, a
 – objętością końcową. Z równania przemiany adiabatycznej w
zmiennych
– objętością końcową. Z równania przemiany adiabatycznej w
zmiennych
 -
-
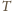

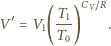
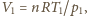
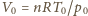 dochodzimy do
wzoru na pracę przy rozprężeniu izotermicznym
dochodzimy do
wzoru na pracę przy rozprężeniu izotermicznym
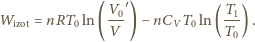
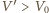 (mamy więc
sprężenie izotermiczne, a nie rozprężenie). Od sumy
(mamy więc
sprężenie izotermiczne, a nie rozprężenie). Od sumy
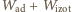 należy
jeszcze odjąć pracę powietrza atmosferycznego
należy
jeszcze odjąć pracę powietrza atmosferycznego
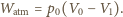
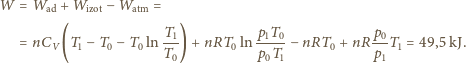
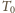 (tzn. zastosować doskonały silnik cieplny korzystający z gazu w
zbiorniku jako grzejnika, a z otoczenia jako chłodnicy), a następnie zastosować
rozprężenie izotermiczne jak poprzednio.
(tzn. zastosować doskonały silnik cieplny korzystający z gazu w
zbiorniku jako grzejnika, a z otoczenia jako chłodnicy), a następnie zastosować
rozprężenie izotermiczne jak poprzednio.