Składanie inwersji z symetrią»Zadanie 9
o zadaniu...
- Zadanie pochodzi z artykułu Składanie inwersji z symetrią
- Publikacja w Delcie: kwiecień 2020
- Publikacja elektroniczna: 1 kwietnia 2020
- Artykuł źródłowy w wersji do druku [application/pdf]: (390 KB)
Trójkąt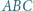 
jest wpisany w okrąg 
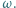Prosta 
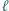jest równoległa do prostej 
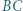i przecina odcinki 
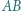i 
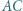odpowiednio w punktach 
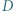i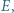 
a okrąg 
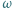w punktach 
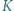i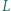 
(gdzie 
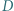leży między punktam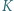i 
i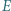 
). Okrąg 
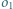jest styczny do odcinków 
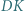i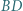 
oraz do okręgu 
; okrąg 
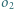jest styczny do odcinków 
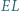i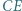 
oraz do okręgu 
Wyznaczyć miejsce geometryczne punktów przecięcia wspólnych stycznych wewnętrznych okręgów 
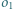i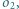 
przy zmieniającym się położeniu prostej 