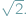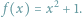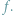Delta mi!

Dawno temu... w czasach bez Internetu, bez gier komputerowych i smartfonów dzieci bawiły się w chowanego. Na początku zabawy trzeba było oczywiście wyznaczyć osobę, która będzie szukać. Uczestnicy ustawiali się w koło i ktoś odliczał: Raz, dwa, trzy, wychodź ty, i wówczas szósta osoba (odliczanka ma 6 sylab) wychodziła z kółka. Procedurę tę powtarzano aż do momentu, gdy w kółku pozostała jedna osoba - to był pierwszy szukający. Istnieje wiele wierszyków-odliczanek. Moją ulubioną jest odliczanka 15-sylabowa: Mama daje jeść, tata daje pić, a ty sobie idź.

Jeżeli określimy dodawanie i mnożenie punktów płaszczyzny, z wyróżnionymi punktami 0 i 1, w sposób przedstawiony na rysunku, to otrzymamy liczby zespolone...

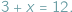Tak jak problemy praktyczne prowadzą do równań, tak równania prowadzą czasem do nowych rodzajów liczb. Ambitny kmieć z czasów Mieszka I, będący właścicielem trzech krów i marzący o nabyciu (lub zdobyciu) dodatkowych sztuk bydła tak, by stać się szanowanym posiadaczem tuzina krów, musiał niewątpliwie rozwiązywać zadanie matematyczne, które dziś zapisujemy równaniem Gdy zamienimy występujące tu liczby miejscami, otrzymamy równanie 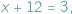które "nie da się rozwiązać": gołym okiem widać, że wśród liczb, za pomocą których zwykliśmy liczyć krowy (czyli liczb naturalnych), nie znajdzie się żadna, która by spełniała to równanie...

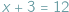Rozwiązywanie równań wymuszało poszerzenie zasobu liczb, jakimi się posługiwano. Równanie można było rozwiązać, posługując się najnaturalniejszymi liczbami, zwanymi zresztą naturalne, ale równanie 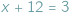wymagało rozszerzenia ich zasobu do liczb całkowitych. Wyjście poza obręb równań pierwszego stopnia pokazało, że do rozwiązania np. równania 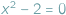nie wystarczą nie tylko liczby całkowite, ale nawet wszystkie liczby wymierne, czyli ułamki 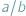zbudowane z liczb całkowitych. Aby uzyskać rozwiązanie, do liczb wymiernych trzeba dołączyć nowe liczby, a wśród nich liczbę niewymierną

Jednym z najstarszych zagadnień matematyki są równania algebraiczne, wśród nich problem znalezienia pierwiastków trójmianu kwadratowego...

Za pomocą kolorowania wielomianów można udowodnić Zasadnicze twierdzenie algebry w zaskakująco elementarny sposób...

Niejeden maturzysta marzy zapewne, żeby na egzaminie dojrzałości rozwiązywać następujące, z pozoru błahe, zadanie: Wyznacz liczbę miejsc zerowych funkcji Abiturienta nie zraziłaby prawdopodobnie nawet drobna przeszkoda, jaką jest wyraźny brak informacji o dziedzinie funkcji  Z uwagi na wszechobecność zbioru liczb rzeczywistych w obecnym programie nauczania wydaje się, że o żadnych zerach mowy być nie może. Nawet słynna „delta” nie jest tu potrzebna.

Jak wiele innych ważnych twierdzeń matematyki, zasadnicze twierdzenie algebry, udowodnione przez Carla Friedricha Gaussa w ostatnim roku osiemnastego stulecia, informuje nas, że pewne obiekty nie istnieją. Mianowicie, nie ma takiego, różnego od stałej, wielomianu zmiennej zespolonej, który nie znikałby w żadnym punkcie płaszczyzny zespolonej

Geometryczną interpretacją ciała liczb zespolonych jest płaszczyzna. Za pomocą liczb zespolonych można opisywać własności figur i przekształceń na płaszczyźnie. Oto kilka przykładów takich zastosowań...