Twierdzenie Chevalleya–Warninga i grafy p-regularne
Rozwiązywanie równań diofantycznych jest jednym z ważniejszych problemów
klasycznej teorii liczb. Czytelnicy tego artykułu na pewno słyszeli o równaniu Pella
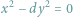 czy równaniu Fermata
czy równaniu Fermata
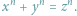
Rozwiązywanie równań diofantycznych jest jednym z ważniejszych problemów
klasycznej teorii liczb. Czytelnicy tego artykułu na pewno słyszeli o równaniu Pella
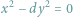 czy równaniu Fermata
czy równaniu Fermata
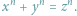
Algorytmy Informatyczny kącik olimpijski
W niedawno wydanej książce W poszukiwaniu wyzwań – zbiorze zadań
z konkursów programistycznych – Filip Wolski opisał rozwiązanie zadania Dwa
przyjęcia z finału XII Olimpiady Informatycznej. W zadaniu tym występuje
 osób, z których niektóre się znają (wiemy które). Chcemy podzielić ten
zbiór na dwa rozłączne podzbiory (przyjęcia) w taki sposób, aby zmaksymalizować
liczbę osób, które mają parzystą liczbę znajomych na przyjęciu, na którym
przebywają...
osób, z których niektóre się znają (wiemy które). Chcemy podzielić ten
zbiór na dwa rozłączne podzbiory (przyjęcia) w taki sposób, aby zmaksymalizować
liczbę osób, które mają parzystą liczbę znajomych na przyjęciu, na którym
przebywają...
W wielu problemach matematycznych warto rozważać elementy ekstremalne – największe, najkrótsze, najbliższe... Metoda ta bywa często przydatna w zadaniach dotyczących punktów płaszczyzny lub grafów, czyli punktów łączonych liniami.
Algebra Konkurs prac uczniowskich
W tym artykule będziemy się zajmowali obliczaniem wyznaczników macierzy
w dowolnym skończonym ciele
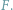 Będziemy także badali, jakie jest
prawdopodobieństwo, że taki wyznacznik dla macierzy z losowo wpisanymi elementami
z ciała
Będziemy także badali, jakie jest
prawdopodobieństwo, że taki wyznacznik dla macierzy z losowo wpisanymi elementami
z ciała
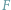 jest różny od
jest różny od
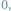 oraz jakie jest prawdopodobieństwo, że
w losowym grafie skierowanym jest nieparzyście wiele pokryć cyklowych.
oraz jakie jest prawdopodobieństwo, że
w losowym grafie skierowanym jest nieparzyście wiele pokryć cyklowych.
Któż z nas nie bawił się jako dziecko w chowanego? Zabawa ta sprawia dzieciom wiele radości, mimo że z algorytmicznego punktu widzenia jest bardzo prosta. Jeżeli bowiem wszyscy ukrywający się czekają uczciwie w swoich kryjówkach, to zawsze uda się ich znaleźć – wystarczy, jeżeli szukający przejrzy wszystkie miejsca.

Obejrzeć płaszczyznę rzutową wcale nie jest łatwo. Z bliska, kiedy widzimy tylko mały fragment, wygląda całkiem jak zwykła płaszczyzna, więc to nic ciekawego. A gdybyśmy chcieli widzieć całą naraz, to musielibyśmy umieć widzieć w przestrzeni przynajmniej czterowymiarowej, bo w naszych trzech wymiarach po prostu nie da się jej porządnie ułożyć. Jeśli nie wierzysz, Czytelniku, wykonaj dający się wziąć w rękę, krawiecki model płaszczyzny rzutowej.
Pierwszy "dowód" twierdzenia o czterech barwach pojawił się w roku 1879. Przedstawił go Alfred Kempe, londyński prawnik. Był to zapewne najsłynniejszy "fałszywy dowód" w całej historii matematyki...
Historia twierdzenia o czterech barwach sięga roku 1852, kiedy to student Francis Guthrie, wiedziony czysto praktycznymi pobudkami, postawił swemu wykładowcy, Augustowi De Morganowi, następujące pytanie: jaka jest najmniejsza liczba kolorów, która wystarcza do pokolorowania dowolnej płaskiej mapy w taki sposób, aby każde dwa państwa, które graniczą ze sobą, otrzymały różne kolory?
W sporcie stosowane są różne systemy prowadzenia rozgrywek. Jednym z nich jest tzw. system pucharowy, w którym zwycięzca meczu kwalifikuje się do dalszych gier, przegrany zaś odpada z turnieju. Aby system był bardziej sprawiedliwy, dokonuje się początkowego rozstawienia przeciwników, tak by teoretycznie najsilniejsi spotkali się jak najpóźniej.
Skojarzenia to bardzo popularny temat. Pojawiają się w różnych miejscach zarówno w informatyce, jak i w matematyce dyskretnej.
Ludzie od niepamiętnych czasów prześcigali się w biciu rekordów w najprzeróżniejszych dziedzinach, od czysto sportowych (szybciej, wyżej, mocniej), poprzez cywilizacyjne (wyższe budowle, większe samoloty, szybsze komputery), aż po całkiem absurdalne, żeby nie powiedzieć głupie.