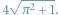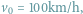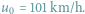Co ma wspólnego cykl (6, 5, 4) z językiem polskim?
Każdej liczbie rzeczywistej możemy przypisać nieskończony ciąg cyfr jej rozwinięcia dziesiętnego. Jak wiadomo, jeżeli ciąg od pewnego miejsca się zapętla, to mamy do czynienia z liczbą wymierną. Inaczej rzecz ujmując, liczby wymierne mają okresowe rozwinięcie dziesiętne. Przyjmujemy tutaj, że tzw. rozwinięcie skończone jest rozwinięciem okresowym - od pewnego miejsca na każdej pozycji występuje wyłącznie cyfra 0.
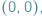 w którym drzewa nie ma, przygląda się temu zjawisku (patrz rysunek). Taki las ciągnie się nieskończenie daleko...
w którym drzewa nie ma, przygląda się temu zjawisku (patrz rysunek). Taki las ciągnie się nieskończenie daleko...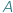 i
i 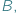 relacją zdefiniowaną pomiędzy tymi dwoma zbiorami matematycy nazywają po prostu podzbiór zbioru wszystkich par elementów, w których pierwszy jest ze zbioru
relacją zdefiniowaną pomiędzy tymi dwoma zbiorami matematycy nazywają po prostu podzbiór zbioru wszystkich par elementów, w których pierwszy jest ze zbioru 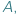 a drugi ze zbioru
a drugi ze zbioru 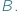 Inaczej mówiąc, element ze zbioru
Inaczej mówiąc, element ze zbioru 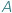 i element ze zbioru
i element ze zbioru 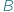 mogą być w danej relacji lub w niej nie być.
mogą być w danej relacji lub w niej nie być.
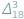 (Z notatnika geniusza) i w tym numerze (Zagnieżdżone pierwiastki) przedstawione są różne zależności liczbowe pochodzące od Ramanujana. Robią ogromne wrażenie, tym bardziej że Ramanujan podał je bez uzasadnień i dla nas mają status natchnionej wizji...
(Z notatnika geniusza) i w tym numerze (Zagnieżdżone pierwiastki) przedstawione są różne zależności liczbowe pochodzące od Ramanujana. Robią ogromne wrażenie, tym bardziej że Ramanujan podał je bez uzasadnień i dla nas mają status natchnionej wizji...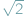 jest niewymierne, czyli że dla żadnej liczby naturalnej
jest niewymierne, czyli że dla żadnej liczby naturalnej 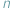 liczba
liczba 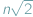 nie jest całkowita.
nie jest całkowita.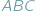 należy umieścić punkt
należy umieścić punkt 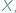 aby suma długości odcinków
aby suma długości odcinków 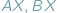 i
i 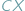 przyjęła najmniejszą wartość.
przyjęła najmniejszą wartość.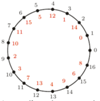

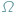 jest zbiorem skończonym i wszystkie zdarzenia jednoelementowe są jednakowo prawdopodobne...
jest zbiorem skończonym i wszystkie zdarzenia jednoelementowe są jednakowo prawdopodobne...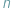 -elementowa tablica
-elementowa tablica ![a[1::n];](/math/temat/informatyka/algorytmy/2016/01/27/Odwracamy_obracamy_/2x-bb064fea4dd2ec318b6920e1034cb0f7c12af931-im-65,9A,A1-FF,FF,FF.gif) którą chcemy odwrócić, czyli spowodować, że jej elementy będą zapisane w kolejności
którą chcemy odwrócić, czyli spowodować, że jej elementy będą zapisane w kolejności ![|a[n];a[n −1]; :::;a[1]:](/math/temat/informatyka/algorytmy/2016/01/27/Odwracamy_obracamy_/3x-bb064fea4dd2ec318b6920e1034cb0f7c12af931-im-65,9A,A1-FF,FF,FF.gif)