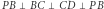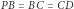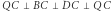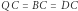Proponowane tematy badań
Przedstawiamy poniżej kilka możliwych tematów prac na Konkurs Prac Uczniowskich z Matematyki. Mamy nadzieję, że uda nam się w ten sposób wytłumaczyć, na czym ów Konkurs polega.
Konkurs Uczniowskich Prac z Matematyki to rywalizacja między samodzielnymi pracami badawczymi uczniów szkół licealnych (nie wykluczamy też gimnazjalistów, ale nie ma dla nich żadnych specjalnych ułatwień). Praca badawcza zaś to opracowanie tematu, który w taki sposób, jaki został zaprezentowany w pracy konkursowej, jeszcze opracowany nie został. Ten sposób musi się różnić merytorycznie (czyli z punktu widzenia matematyki) od ujęć dostępnych w literaturze, niezależnie od jej nośnika (a więc publikacji papierowej, internetowej, filmowej itd.). Nie interesuje nas zatem inne ułożenie redakcyjne, opatrzenie innymi komentarzami rzeczy gotowych.
Są zresztą konkursy na twórcze opracowanie tematów matematycznych zaproponowanych przez organizatorów tych konkursów.
Matematyka jest jednak na tyle bogata, że każdy może znaleźć dla siebie wiele nierozwiązanych problemów i nie wszystkie z nich wymagają profesjonalnej techniki i rutyny - często błysk natchnienia, muśnięcie skrzydłem muzy wystarczy, by odkryć coś nowego. Zaproponowane w tej wkładce tematy będą sugerowały pewne okolice, w których można takich odkryć poszukiwać. Nie mamy pewności, że te odkrycia tam są, ale mamy pewną rutynę, która pozwala nam wskazywać te, a nie inne, okolice tak, jak geolog może sugerować, gdzie szukać złota czy diamentów.
Laureaci naszych Konkursów, odbywających się już od ćwierć wieku, rozmaicie ułożyli swoje życie. Są jednak wśród nich wybitni uczeni, a kilku młodszych ma "w kieszeni" medal z urządzanego przez Unię Europejską konkursu na Młodego Uczonego Europejskiego. Konkurs zaowocował także wieloma publikacjami w czasopismach fachowych.
Zapraszamy do udziału.
***
***
Porównanie metod na obliczenie pierwiastków
Istnieją różne metody pozwalające "na piechotę" obliczyć pierwiastek z danej liczby (czyli bez użycia kalkulatora). Jednym z nich jest pierwiastkowanie pod kreską (opisane tutaj), innym Metoda Newtona.
Przy ich porównywaniu warto uwzględnić, która z tych metod jest szybsza tj. jeżeli chcemy uzyskać wynik z zadaną z góry dokładnością, która z nich potrzebuje mniejszej liczby kroków. Która z tych metod jest szybsza dla pierwiastka 2-stopnia? A 3-go, 4-go,  -tego?
-tego?
Oblicz wartość funkcji
Oczywiście istnieje wiele funkcji, dla których nie da się obliczyć ich konkretnych wartości i to już dla, zdawałoby się, najprostszych argumentów. Niektóre z takich problemów mają renomę niesłychanie trudnych (choćby problem obliczania liczb Ramseya - patrz np. Delta 1/2002 - powszechnie się sądzi, że znalezienie wartości, powiedzmy, 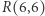 długo jeszcze przekraczać będzie ludzkie możliwości).
długo jeszcze przekraczać będzie ludzkie możliwości).
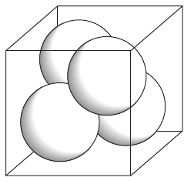
Ale czasem funkcja nie ma złej sławy. Weźmy choćby funkcję, która odpowiada na pytanie, jak wielkie kule mogą się zmieścić w sześcianie.
Dokładniej: w sześciennym pudełku o krawędzi 1 znajduje się 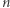 jednakowych kul; funkcja
jednakowych kul; funkcja 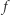 przyporządkowuje każdemu
przyporządkowuje każdemu  największą wartość
największą wartość 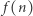 średnicy kul -
średnicy kul - 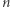 kul o takiej średnicy zmieści się jeszcze w pudełku,
kul o takiej średnicy zmieści się jeszcze w pudełku, 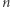 kul o większej średnicy umieścić się w pudełku nie da.
kul o większej średnicy umieścić się w pudełku nie da.
Już z samej definicji widać, że 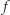 jest funkcją nierosnącą.
jest funkcją nierosnącą.
Oczywiście 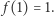 Nie jest specjalnie trudno sprawdzić, że
Nie jest specjalnie trudno sprawdzić, że
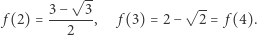
I tu jest zaskoczenie: funkcja nie jest ściśle malejąca.
Bez trudu można zauważyć, że np. 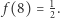 Ale jak obliczyć wartości funkcji dla 5, 6, 7, czy innych wartości nie będących sześcianami? A jak często funkcja przyjmuje te same wartości dla kolejnych liczb naturalnych? Czy "postoje" mogą być dłuższe? Jak długie?
Ale jak obliczyć wartości funkcji dla 5, 6, 7, czy innych wartości nie będących sześcianami? A jak często funkcja przyjmuje te same wartości dla kolejnych liczb naturalnych? Czy "postoje" mogą być dłuższe? Jak długie?
Słowem, pytań jest wiele. Wiele jest też naturalnie zdefiniowanych funkcji do zbadania.
Marek Kordos
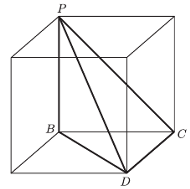
Rys. 1  i
i 
Wypełnianie przestrzeni
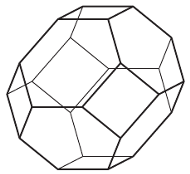
Rys. 2
Nie jest trudno wypełnić szczelnie przestrzeń jednakowymi sześcianami - każdy wskaże bez trudu kilka sposobów. Jest niemożliwe szczelne wypełnienie przestrzeni jednakowymi czworościanami foremnymi - co drugi potrafi to udowodnić. Trochę trudniej będzie wykazać, że pokazanym na rysunku 1 czworościanem przestrzeń można szczelnie wypełnić.
W Kalejdoskopie Matematycznym Steinhausa (i w Delcie 9/1996) można znaleźć informacje, jak wypełnić przestrzeń czternastościanami powstałymi przez obcięcie ośmiościanowi foremnemu wszystkich rogów tak, aby wszystkie krawędzie pozostałego wielościanu były równej długości (Rys. 2).
Kolekcja wypełniających przestrzeń wielościanów wypukłych nie jest pełna. Nie wiadomo już np. jak wyglądają wszystkie czworościany, którymi można szczelnie wypełnić przestrzeń. Albo np. pięciościany. Albo czy istnieje górne ograniczenie na liczbę ścian wielościanu wypukłego, którego kopiami da się szczelnie wypełnić przestrzeń? Pytań można postawić bardzo wiele i zapewne na wiele z nich uda się znaleźć odpowiedź.
Oczywiście problem był i jest badany. Można więc znaleźć informacje o tym, co powszechnie wiadomo. Żadna całościowa teoria na ten temat jednak nie została zbudowana.
Marek Kordos
Przestrzenne tangramy
Tangram to takie płaskie kostki, z których można ułożyć różne figury. Przestrzenny tangram to takie klocki przestrzenne, z których można ułożyć różne wielościany. Pamiętajmy, że za każdym razem muszą być użyte wszystkie klocki. Czyli równoważne "tangramowo" wielościany mają równe objętości.
Zażądajmy dodatkowo, aby ułożony z takich kostek wielościan był wypukły. Nie jest oczywiste, czy z każdego takiego tangramu można ułożyć choćby dwa różne wypukłe wielościany. Czasami jednak tak się zdarza. Np. czworościan z rysunku 1 można pociąć na mniejsze części - wielościany, z których da się ułożyć sześcian. Nie wiadomo jednak, jaka jest najmniejsza liczba tych mniejszych części.
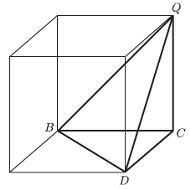
Rys. 3 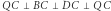 i
i 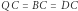
Ale żadne pocięcie czworościanu foremnego na skończoną liczbę klocków wielościennych nie pozwoli ułożyć z tych klocków sześcianu. Podobnie, żadne pocięcie na skończoną liczbę wielościennych klocków czworościanu z rysunku 3 nie pozwoli na ułożenie z nich sześcianu. Ale czy jakieś klocki z tego czworościanu pozwolą na ułożenie z nich czworościanu foremnego?
Zauważmy, że mamy dość zaskakujący wynik: czworościany z rysunków 1 i 3 nie są "tangramowo" równoważne.
A czy któryś z tych czworościanów jest "tangramowo" równoważny z czternastościanem z rysunku 2?
Dla dowolnego konkretnego wielościanu można poszukać jak najwięcej wielościanów, z którymi jest "tangramowo" równoważny.
Istnieje dość rozwinięta teoria zajmująca się takimi tangramami. Jednak rezultatów dotyczących konkretnych wielościanów jest w niej mało. Stąd pole do popisu.
Marek Kordos
Liczby niedoskonałe
Pitagorejczycy nadawali duże znaczenie liczbom doskonałym, czyli takim liczbom naturalnym, które są równe sumie swoich dzielników właściwych (różnych od samej tej liczby). Nazwijmy liczbę naturalną poddoskonałą, gdy suma jej dodatnich dzielników właściwych jest od niej mniejsza (np. 4), a naddoskonałą - gdy suma jej dodatnich dzielników właściwych jest od niej większa (np. 12). Łatwo zauważyć, że liczb poddoskonałych jest nieskończenie wiele, ponieważ każda liczba pierwsza jest poddoskonała. Czy liczb naddoskonałych też jest nieskończenie wiele? Czy istnieją dowolnie długie ciągi kolejnych liczb naddoskonałych? A liczb poddoskonałych? Które liczby - poddoskonałe czy naddoskonałe - są gęściej rozmieszczone wśród liczb naturalnych? A może istnieje granica stosunku liczby liczb naddoskonałych nie większych od  do
do 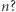 Pytania można mnożyć (niemal) bez ograniczeń.
Pytania można mnożyć (niemal) bez ograniczeń.
Wiktor Bartol
Znaczące współczynniki
Wykres funkcji liniowej
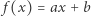
zależy od każdego ze współczynników:  decyduje o nachyleniu prostej,
decyduje o nachyleniu prostej, 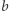 o jej położeniu względem osi współrzędnych. Wiemy, co się dzieje z funkcją kwadratową postaci
o jej położeniu względem osi współrzędnych. Wiemy, co się dzieje z funkcją kwadratową postaci
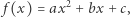
gdy zmieniamy współczynnik 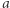 : ramiona paraboli będą zmieniać nachylenie, może nastąpić odwrócenie paraboli. Wiemy także, co się stanie, gdy zmieniać będziemy współczynnik
: ramiona paraboli będą zmieniać nachylenie, może nastąpić odwrócenie paraboli. Wiemy także, co się stanie, gdy zmieniać będziemy współczynnik 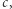 a nawet potrafimy powiedzieć, co się dzieje z parabolą, gdy zmieniamy tylko współczynnik
a nawet potrafimy powiedzieć, co się dzieje z parabolą, gdy zmieniamy tylko współczynnik 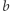 (właśnie, co?). Czy można w podobny sposób opisać znaczenia współczynników wielomianów wyższych stopni, poczynając od stopnia trzeciego? Jak wpływa na wykres zmiana każdego z nich? Pewne intuicje można sobie zapewne wyrobić na podstawie wykresów oglądanych na ekranie komputera lub kalkulatora graficznego, ale czy można je uściślić i opisać matematycznie?
(właśnie, co?). Czy można w podobny sposób opisać znaczenia współczynników wielomianów wyższych stopni, poczynając od stopnia trzeciego? Jak wpływa na wykres zmiana każdego z nich? Pewne intuicje można sobie zapewne wyrobić na podstawie wykresów oglądanych na ekranie komputera lub kalkulatora graficznego, ale czy można je uściślić i opisać matematycznie?
Wiktor Bartol
Ukryta podzielność
Kiedy wartości wielomianu o współczynnikach całkowitych są dla wszystkich całkowitych argumentów podzielne przez ustaloną liczbę 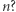 Na pewno wtedy, gdy wszystkie współczynniki danego wielomianu są podzielne przez
Na pewno wtedy, gdy wszystkie współczynniki danego wielomianu są podzielne przez 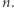 To tak oczywisty przypadek, że nawet nie warto o nim wspominać. Ale czy tylko wtedy? Co będzie, kiedy współczynniki wielomianu nie mają wspólnego dzielnika większego od 1? Wtedy mimo wszystko wartości wielomianu mogą być podzielne przez ustaloną liczbę większą od 1!
To tak oczywisty przypadek, że nawet nie warto o nim wspominać. Ale czy tylko wtedy? Co będzie, kiedy współczynniki wielomianu nie mają wspólnego dzielnika większego od 1? Wtedy mimo wszystko wartości wielomianu mogą być podzielne przez ustaloną liczbę większą od 1!
Najprostszy przykład to wielomian 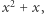 którego wartość dla dowolnej liczby całkowitej
którego wartość dla dowolnej liczby całkowitej 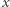 jest parzysta. Podobnie, wartości wielomianu
jest parzysta. Podobnie, wartości wielomianu 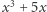 są zawsze podzielne przez 6.
są zawsze podzielne przez 6.
I stąd już możesz, drogi Czytelniku, wypłynąć na szerokie wody badacza ukrytych podzielności. Możesz znaleźć mnóstwo takich wielomianów. Może uda Ci się je jakoś sklasyfikować lub udowodnić jakieś twierdzenia o tym, kiedy taka ukryta podzielność na pewno występuje albo kiedy nie występuje. A jak tego będzie mało, zawsze można uciec w wielomiany wielu zmiennych, np. wartość wielomianu 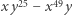 dla dowolnych całkowitych argumentów
dla dowolnych całkowitych argumentów  i
i 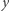 jest podzielna przez 2730.
jest podzielna przez 2730.
Jarosław Wróblewski
Wyznaczniki dużych macierzy
Na ogół niewiele da się powiedzieć o wyznaczniku dużej macierzy poza podaniem definicji wyznacznika lub żmudnym wyliczeniem go w konkretnym przypadku.
Ale jeżeli macierz jest szczególnej postaci...
Co to znaczy "szczególnej postaci"? A to już zależy od Waszej inwencji twórczej.
Wyobraźmy sobie, że mamy macierz zbudowaną według prostego przepisu (a raczej ciąg 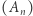 macierzy o wzrastających rozmiarach).
macierzy o wzrastających rozmiarach).
Na przykład macierz 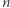 na
na  postaci
postaci
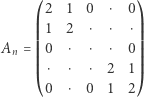
ma dwójki na przekątnej, jedynki bezpośrednio pod i nad przekątną, a poza tym zera.
Ile jest równy wyznacznik macierzy 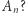 Nietrudno dostrzec, że
Nietrudno dostrzec, że 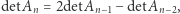 skąd otrzymujemy
skąd otrzymujemy 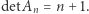
A czemu jest równy wyznacznik macierzy
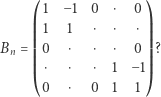
A macierzy
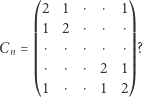
A innych, wymyślonych przez Was macierzy?
Jarosław Wróblewski
A jednak całkowite
Liczba
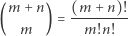
jest całkowita dla dowolnych liczb naturalnych 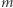 i
i 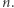 Fakt ten i niezliczone dowody jego są tak znane, że przytaczać ich po prostu nie wypada.
Fakt ten i niezliczone dowody jego są tak znane, że przytaczać ich po prostu nie wypada.
Jeśli jednak rozważymy liczbę
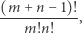
to na ogół nie będzie ona całkowita. Chyba że w jakiś szczególny sposób powiążemy 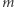 i
i 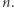
Na przykład liczba
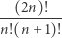
jest całkowita dla każdego 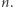 Nie jest mi znany kombinatoryczny dowód tego faktu, można go jednak udowodnić, wykorzystując nierówność
Nie jest mi znany kombinatoryczny dowód tego faktu, można go jednak udowodnić, wykorzystując nierówność
![[n] + [n-+1] ⩽ [2n-], k k k](/math/delta/redakcja/konkurs_prac_uczniowskich/proponowane_tematy_badan/3x-2ddf75b5359f03cb25a818a3ad1e587d7508974b-dm-33,33,33-FF,FF,FF.gif)
gdzie ![[x]](/math/delta/redakcja/konkurs_prac_uczniowskich/proponowane_tematy_badan/4x-2ddf75b5359f03cb25a818a3ad1e587d7508974b-im-33,33,33-FF,FF,FF.gif) oznacza część całkowitą liczby
oznacza część całkowitą liczby 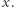
I tu zadanie dla Ciebie, drogi Czytelniku. Znaleźć inne sytuacje, w których liczba
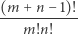
jest całkowita. Mogą to być warunki na 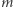 i
i 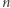 (np.
(np. 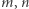 większe od 0 i
większe od 0 i 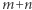 pierwsza) lub przykłady wyrażeń postaci
pierwsza) lub przykłady wyrażeń postaci
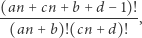
(gdzie 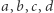 są ustalone) przyjmujących wartość całkowitą dla każdego
są ustalone) przyjmujących wartość całkowitą dla każdego 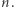 Może uda Ci się udowodnić twierdzenia postaci jak
Może uda Ci się udowodnić twierdzenia postaci jak 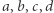 są takie a takie, to jest dobrze, a jak są takie a takie, to jest źle.
są takie a takie, to jest dobrze, a jak są takie a takie, to jest źle.

Ciekawa byłaby też odpowiedź na pytanie, czy istnieją takie 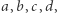 że liczba
że liczba
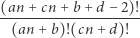
jest całkowita dla każdego  lub rozsądnie ogólny warunek na
lub rozsądnie ogólny warunek na 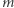 i
i  pociągający całkowitość liczby
pociągający całkowitość liczby
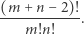
Jarosław Wróblewski
Magia liczby
Znana jest konstrukcja liczby mega pochodząca od Hugona Steinhausa i liczby moser pochodząca od Leo Mosera. Liczba 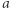 w trójkącie to prostu liczba
w trójkącie to prostu liczba  Liczba
Liczba 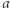 w prostokącie to liczba
w prostokącie to liczba  otoczona
otoczona 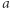 trójkątami.
trójkątami.
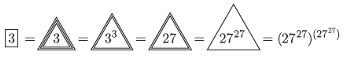
Liczba 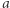 w pięciokącie to liczba
w pięciokącie to liczba 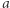 otoczona
otoczona  prostokątami. Liczba mega to liczba 2 w pięciokącie. Moser to liczba 2 otoczona mega-kątem. Skonstruujmy inną serię wielkich liczb. Dla dowolnych liczb naturalnych
prostokątami. Liczba mega to liczba 2 w pięciokącie. Moser to liczba 2 otoczona mega-kątem. Skonstruujmy inną serię wielkich liczb. Dla dowolnych liczb naturalnych 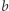 i
i  przyjmijmy
przyjmijmy
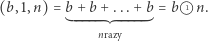
Oczywiście znaczek 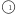 zastępuje tu znak mnożenia. Dla
zastępuje tu znak mnożenia. Dla 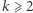 przyjmijmy
przyjmijmy
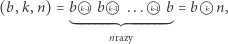
umawiając się, że działania wykonujemy "od tyłu" (tzn. od prawej do lewej). Jak za pomocą liczb 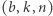 oszacować z dołu i z góry liczbę mega i moser? A może skonstruujecie inne liczby, które przydadzą się w szacunkach?
oszacować z dołu i z góry liczbę mega i moser? A może skonstruujecie inne liczby, które przydadzą się w szacunkach?
Przemysław Panek i Witold Sadowski
Trójkolorowe gry Hackenbush
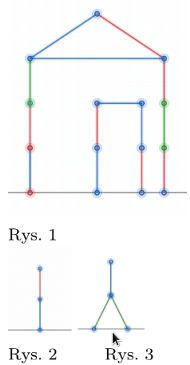
Hackenbush jest grą wymyśloną przez Johna H. Conway'a polegającą na zmazywaniu narysowanych na planszy linii (względnie zabieraniu patyczków). Wszystkie linie muszą w trakcie gry być połączone z umownym podłożem (ewentualnie ramką obrazka), a gdy takie połączenie tracą są zmazywane. Linie w grze mają kilka kolorów, które mają znaczenie w grze. Gracze Niebieski i Czerwony mogą zmazywać linie w ich kolorze. Ponadto niektóre linie mogą być koloru zielonego, który mogą zmazywać obaj gracze. Ruchy wykonujemy naprzemian zmazując jedną linię (i ewentualną resztę, która traci kontakt z podłożem). Ten, kto nie może już wykonać ruchu przegrywa, czyli wygrywa ten, kto wykonał ostatni ruch. Pozycja startowa może wyglądać na przykład tak, jak na rysunku 1.
Oczywistym zatem wydaje się fakt, że opłaca się oszczędzać linie własnego koloru, a odrywać kreski przeciwnika, jeśli mamy taką możliwość. Jeśli odrywanie przez przeciwników nie zachodzi, to możemy łatwo obliczyć przewagę wyrażoną w ruchach. Okazuje się, że może być też przewaga ułamkowa na przykład w pozycji przedstawionej na rysunku 2 gracz niebieski ma przewagę odpowiadającą dokładnie połowie swojego ruchu, bo jeśli zestawimy dwie takie gry z grą, w której to czerwony ma jeden ruch przewagi, to zawsze wygra drugi gracz (czyli przewaga jest zerowa). Okazuje się, że w sytuacji, gdy na obrazku są tylko niebieskie i czerwone linie nigdy nie wygrywa zaczynający, a przewagę można wyrazić pewnym ułamkiem.
Mniej wyjaśnione są sytuacje, gdzie dochodzi ten zielony kolor. Ciekawa jest pozycja pokazana na rysunku 3. Co prawda niebieski zawsze wygra, czyli ma przewagę, ale ta przewaga jest mniejsza niź jakakolwiek ułamkowa przewaga, którą mógłby mieć w grze czerwono-niebieskiej. Takich nieskończenie małych zbudowanych z kilku raptem kresek można budować więcej, a wyjaśnienie jak działają w jakiś sensowny sposób, to właśnie temat do badania. Zdaje się, że nie ma nawet dobrego objaśnienia jak to działa dla gier składających się z samych trójkolorowych pędów bambusa, a to najprostsza sytuacja w czerwono-niebieskim przypadku.
Wieże potęgowe
Oznaczmy wieżę potęgową 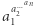 przez
przez ![|[a1;a2;...;an],](/math/delta/redakcja/konkurs_prac_uczniowskich/proponowane_tematy_badan/2x-e229f15db7dda047385cd283b123a5d3c582094c-im-33,33,33-FF,FF,FF.gif) gdzie
gdzie 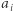 jest liczbą całkowitą dla
jest liczbą całkowitą dla 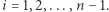 Sposobem na porównanie wartości dwóch wież potęgowych jest zapisanie ich w postaci
Sposobem na porównanie wartości dwóch wież potęgowych jest zapisanie ich w postaci
![[10;10;...;10;xi], gdzie xi ∈[1,10).](/math/delta/redakcja/konkurs_prac_uczniowskich/proponowane_tematy_badan/5x-e229f15db7dda047385cd283b123a5d3c582094c-dm-33,33,33-FF,FF,FF.gif) |
(1) |
Oczywiście nie od razu wiadomo ile dziesiątek należy zapisać - szczegóły można znaleźć w [1]. Jednak mając już dwie wieże w postaci (1) albo będą miały one taką samą liczbę dziesiątek - i wtedy porównując ostatni wyraz łatwo stwierdzić, która jest większa (lub czy są równe) - albo będą różniły się liczbą dziesiątek, i wtedy też sprawa jest jasna.
Zapisywanie wież w postaci (1) ma wiele zaskakujących własności. Na przykład dla 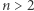 zachodzi następujące szacowanie
zachodzi następujące szacowanie ![[9;9;...;9]≈ [10;10;...;10;8,568]. n n−1](/math/delta/redakcja/konkurs_prac_uczniowskich/proponowane_tematy_badan/2x-ce168349d8bef501853afdc9e83c2589820f4aaa-im-33,33,33-FF,FF,FF.gif) A nawet więcej:
A nawet więcej:
Twierdzenie. Niech wieże ![|[9;9;...;9] n](/math/delta/redakcja/konkurs_prac_uczniowskich/proponowane_tematy_badan/3x-ce168349d8bef501853afdc9e83c2589820f4aaa-im-33,33,33-FF,FF,FF.gif) będą w postaci
będą w postaci ![|[10;10;...;10;xn]. n− 1](/math/delta/redakcja/konkurs_prac_uczniowskich/proponowane_tematy_badan/4x-ce168349d8bef501853afdc9e83c2589820f4aaa-im-33,33,33-FF,FF,FF.gif) Istnieja granica
Istnieja granica 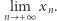
Czy powyższe stwierdzenie można uogólnić? Tj. podać inne przykłady wież, takich że granica ostatnich wyrazów 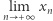 istnieje? Co w przypadku, gdy wyrazy w wieży pojawiają się okresowo?
istnieje? Co w przypadku, gdy wyrazy w wieży pojawiają się okresowo?