Dwa dowody jednego twierdzenia
Zbiór wszystkich liczb rzeczywistych 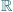 nie jest równoliczny ze zbiorem wszystkich liczb naturalnych
nie jest równoliczny ze zbiorem wszystkich liczb naturalnych 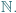
Zbiór wszystkich liczb rzeczywistych 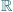 nie jest równoliczny ze zbiorem wszystkich liczb naturalnych
nie jest równoliczny ze zbiorem wszystkich liczb naturalnych 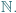
Każda nauka ścisła ma własne metody potwierdzania swoich tez. Dla większości z nich weryfikacja twierdzeń polega na konfrontacji z rzeczywistością. Matematyka jest jedyną z tych nauk, w której owa rzeczywistość nie jest ostateczną (ani jakąkolwiek) metodą sprawdzania zdań aspirujących do wzbogacenia zasobu wiedzy matematycznej. Weryfikatorem twierdzeń jest dowód. Mowa tu o tzw. matematyce czystej lub teoretycznej; zauważmy jednak, że fizyczna rzeczywistość weryfikuje stosowalność instrumentów matematycznych, nie ich wartość matematyczną.

David Hilbert (1862-1943)
Matematyka bardzo się w XIX wieku zmieniła. Algebra, badająca dotąd przede wszystkim metody rozwiązywania równań wielomianowych, dzięki pracom Evariste'a Galois, George'a Boole'a i innych wytworzyła struktury abstrakcyjne: grupy, pierścienie, algebry Boole'a, oderwane od obliczeń liczbowych, reprezentujące za to pewne ogólne własności działań (na dowolnych obiektach). Geometria utraciła euklidesową jednoznaczność, odnajdując się w światach dotąd nieznanych i nieprzewidywanych, zwanych geometriami nieeuklidesowymi. Analiza, nabierając coraz bardziej potrzebnej ścisłości, wyszła poza granice intuicji, uwzględniając szerszy repertuar funkcji (niegdyś uważanych za ciągłe z definicji) i dopuszczając zaskakujące konstrukcje, jak choćby funkcje wszędzie ciągłe i nigdzie nieróżniczkowalne.
Zawód matematyka, jak powiada jeden z uprawiających go kolegów, polega na rozwiązywaniu zadań z treścią. Takich zadań pełne są podręczniki do nauczania matematyki na różnych poziomach edukacji. Zazwyczaj jednak matematyk zajmuje się zadaniami, których do tej pory nikt nie rozwiązał; najczęściej zaczynają się one od "wykaż, że". Skąd się biorą? Z zadziwienia, z zachwytu, wreszcie z ciekawości, która rodzi pytania: "jak?", "dlaczego?". Takie zadziwienie, taki zachwyt czy taka ciekawość pojawiają się w każdym wieku, wystarczy mieć otwarte oczy i otwarty umysł, wsparte zainteresowaniem popychającym do dążenia tropem zauważonych śladów.
Matematyka, zwłaszcza tzw. szkolna, wypracowała przez lata procedury rozwiązywania określonego typu zadań. Gdy rozpoznajemy problem jako równanie kwadratowe, w głowie pojawia się hasło "bekwadratminusczteryace" i już wszystko wiadomo, niezależnie od tego, jak w rzeczywistości nazwaliśmy współczynniki funkcji kwadratowej...

Gry, zagadki, paradoksy Mała Delta
Legenda powiada, że gdy bóg Brahma po raz pierwszy poruszył czas, umieścił na jednej z trzech diamentowych igieł, umocowanych na wspólnej podstawce, 64 złote krążki. Na podstawce spoczywał krążek najszerszy, a nad nim lśniły pozostałe o coraz mniejszych średnicach. Bóg polecił mnichom z górskiej samotni, by bez spoczynku przekładali krążki, tak aby wszystkie znalazły się na drugiej diamentowej igle, z zachowaniem tego samego ułożenia. Gdy zadanie zostanie zakończone, nastąpi koniec pierwszego świata, a na następny, wskrzeszony przez Brahmę, wypadnie czekać wiele tysięcy lat...
Gry, zagadki, paradoksy Drobiazgi
Numer Delty poświęcony paradoksom nie byłby kompletny, gdyby nie pojawiła się w nim paradoksalna gra. Przyjrzyjmy się zatem pewnej grze, inspirowanej paradoksami teoriomnogościowymi, które rozkwitły w początkach XX wieku.
Gdy w połowie XIX wieku odkryto geometrie nieeuklidesowe, zainteresowanie matematyków zaczęło zwracać się w stronę podstaw matematyki. Na jakich podstawach można lub należy oprzeć matematykę? Na tym tle zrodził się w latach 20. XX wieku tzw. program Hilberta, postulujący zbudowanie sformalizowanej matematyki na fundamencie aksjomatycznym i wyprowadzanie z aksjomatów twierdzeń jedynie za pomocą ściśle określonych reguł. Tak zbudowana teoria powinna być zupełna i niesprzeczna i te jej własności powinny dać się udowodnić.

Gry, zagadki, paradoksy Recenzje
Ian Stewart, którego czytelnikom Delty przedstawiać nie trzeba, stosował w swoich książkach różne formy literackie: eseje, wykłady, listy... Tym razem wybrał formę najprostszą: zbiór wszelkiego rodzaju ciekawostek, zadań, informacji, także tytułowych zagadek (do których książka się absolutnie nie ogranicza), wszystko pod wspólnym hasłem: Matematyka, której uczyliście się w szkole, to jeszcze nie wszystko
Historia i filozofia nauk O tym, czego nie ma
Filozof i logik angielski Bertrand Russell określił matematykę jako dziedzinę, w której „nie wiadomo, o czym się mówi i czy to, co się mówi, jest prawdą”. Ten zgrabny opis miał wyrażać – w skrócie właściwym aforyzmom – fakt, iż matematyka jest nauką abstrakcyjną, niezależną od rzeczywistości i zajmującą się wyprowadzaniem (dowodzeniem) twierdzeń na podstawie ściśle określonego sposobu wnioskowania, nie interesuje jej natomiast związek tych twierdzeń z tzw. życiem.
Teoria Mnogości O tym, czego nie ma
Cóż prostszego, jak stworzyć zbiór z dowolnych prawdziwych lub wymyślonych obiektów! Czyż zbiór nie jest po prostu pewną konstrukcją myślową? Wystarczy zatem pomyśleć o owych obiektach jako o elementach jednego zbioru – i już.
Gry, zagadki, paradoksy Mała Delta
Nierzadko zbywamy kandydatów na twierdzenia matematyczne niemal pogardliwym
określeniem: oczywiste! Liczba
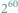 jest większa od
jest większa od
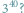 Oczywiste!
Środek okręgu opisanego na trójkącie leży wewnątrz trójkąta? Oczywiste!
Oczywiste!
Środek okręgu opisanego na trójkącie leży wewnątrz trójkąta? Oczywiste!
Tangram to stara chińska zabawa, polegająca na układaniu zadanych figur z siedmiu klocków, ułożonych na rysunku 1 w kwadrat.
Gry, zagadki, paradoksy Mała Delta
Większość znanych gier ma tę miłą własność, że kończy się po skończonej liczbie ruchów. Gdyby jednak gra polegała na tym, że gracze na przemian wskazują liczby naturalne, a wygrana na tym, że przeciwnik nie może już wskazać liczby większej, to taka gra musiałaby trwać nieskończenie długo (jeśli na chwilę zapomnimy o prawach biologii...).
Definicja paradoksu obejmuje różne sytuacje, powody i postacie paradoksów. Wobec tej różnorodności form spróbujmy dokonać klasyfikacji.
Jeśli macie w biurku trzy szuflady, a chcecie do nich włożyć zeszyty z, powiedzmy, sześciu przedmiotów, to nie ma rady: w co najmniej jednej szufladzie muszą znaleźć się zeszyty z co najmniej dwóch przedmiotów.