Delta mi!

Indukcja pozaskończona wykorzystywana jest w dowodach istnienia różnych obiektów matematycznych. Główną częścią tego typu dowodu jest definicja indukcyjna (inaczej: rekurencyjna) funkcji.

Korzenie teorii miary sięgają tak podstawowych pojęć, jak długość (np. odcinka), pole (np. koła) i objętość (np. kuli). Wraz z rozwojem matematyki konieczne stało się uogólnienie tych pojęć w taki sposób, żeby dało się „zmierzyć” coraz bardziej skomplikowane podzbiory danej przestrzeni – na przykład prostej rzeczywistej 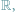do której w tym artykule ograniczymy nasze rozważania.