Delta mi!

- Hop, hop, jest tam kto? - krzyczy 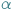otoczona tłumem.
- Hop, hop, spójrz tutaj. - odpowiada 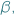który co prawda słyszy 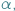ale zupełnie jej nie widzi.
- Jakie "tutaj"? Przecież dookoła nie ma żywej duszy. - 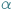otoczona tłumem po raz kolejny usiłuje dostrzec 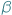pośród otaczającej pustki.

Stoimy u progu nieskończenie milowego, nad wyraz uporządkowanego lasu. Najlepszym miejscem na uporządkowany las jest oczywiście układ współrzędnych. Pnie drzew, które są odcinkami, umieszczone są w punktach o współrzędnych całkowitych nieujemnych. Nasz wzrok z punktu w którym drzewa nie ma, przygląda się temu zjawisku (patrz rysunek). Taki las ciągnie się nieskończenie daleko...

Wyobraźmy sobie, że przyszło nam żeglować po jeziorze pod wiatr...

Spójrzmy na poniższe obrazki i nie zastanawiając się, co właściwie przedstawiają, spróbujmy zgadnąć, jak powinien wyglądać kolejny.

Conway's Soldiers to jednoosobowa łamigłówka, w której żołnierze (pionki) przedostają się na terytorium wroga i chcą wkroczyć jak najdalej. Na nieskończonej szachownicy, z zaznaczoną "na środku" poziomą granicą, pionki przeskakują jeden nad drugim. Dokładniej: ruch polega na przeskoczeniu pionkiem nad innym znajdującym się na sąsiadującym polu - tylko poziomo lub pionowo - i zdjęciu pionka, który został przeskoczony.

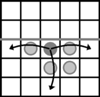
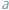Wyobraźmy sobie, że trafiliśmy do dziwnego kraju, w którym jedynymi dostępnymi środkami płatniczymi są monety o nominałach i 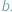Formy płatności nie rozwinęły się na tyle, żeby płacić kartą lub czekiem, na domiar złego wybraliśmy się do cukierni, w której kasa jest zupełnie pusta i sprzedawca nie może wydać nam reszty. Nie chcąc tracić swoich złociaków, rozglądamy się za pysznościami w cenach 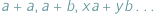Niektórych kwot, oczywiście, nie daje się uzyskać z nominałów 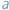i a niektóre można otrzymać na wiele sposobów.

Zabawmy się Pitagorasem, budując ustrojstwo przedstawione obok...

Pętle na rysunku 1 przedstawiają ten sam sznurek...

Zamiast analizować, czy gra jest sprawiedliwa, czy nie, zamiast szukać najlepszych strategii graczy, można stworzyć pewną maszynę, która część tej pracy wykona za nas. Trzeba jej objaśnić zasady, a potem z nią grać, niekoniecznie najlepiej - w końcu jeszcze nie przeanalizowaliśmy gry. Maszyna, grając, zapamiętując i wyciągając wnioski z przegranych oraz wygranych (co śmiało można zakwalifikować jako uczenie się), prędzej czy później zorientuje się, jak grać możliwie najlepiej, a więc ogrywać nas, o ile to tylko możliwe.

Taka sobie niewinnie wyglądająca bryłka. Ot, powstała z obrotu kwadratu dookoła jego przekątnej, przecięcia tego, co powstało, na dwie identyczne części (wzdłuż płaszczyzny kwadratu), przekręceniu połowy o i doklejeniu do drugiej części (czekającej w tym czasie w bezruchu). Szczęśliwa całość - sferostożek (ang. sphericon).

Dym zaczął radośnie buchać ze starego, ceglanego komina. To znak, że Czerwony Kapturek, właścicielka najbardziej czerwonego kubraczka w stumilowym lesie, rozpoczęła już swoje wyśmienite wypieki. Świeżutkie bułeczki dostaną wszyscy ci i tylko ci mieszkańcy lasu, którzy sami nie robią dziś wypieków...

Dawno, dawno temu za górami, za lasami na Euklidesowych Równinach żyło sobie koło. Niezmiernie było dumne ze swej stałej szerokości. Chadzało ścieżkami, które miały szerokość równą jego średnicy, i jako jedyna figura zamieszkująca równiny mogło kręcić się przy tym jak szalone, stale podpierając obie krawędzie ścieżki.

Bryła to stworzenie, z którym większość z nas poznała się w szkole podstawowej i które było przez nas oswajane przez kolejne lata edukacji. Znamy bliżej różne rodziny brył, takie jak wielościany, graniastosłupy, bryły obrotowe, foremne, platońskie. Oczywiście, można produkować nowe stworzenia, łącząc czy tnąc "podstawowe" gatunki, a jedynym ograniczeniem jest nasza wyobraźnia.

Wyobraźmy sobie, że trafiliśmy do dziwnego kraju, w którym jedynymi dostępnymi środkami płatniczymi są monety o nominałach 5 i 9. Formy płatności nie rozwinęły się na tyle, żeby płacić kartą lub czekiem, na domiar złego wybraliśmy się do cukierni, w której kasa jest zupełnie pusta i sprzedawca nie może wydać nam reszty...