Problem 153. z Księgi Szkockiej

Fot. Wiesław Szlenk
Stanisław Mazur i Per Enflo (1972)
Zdjęcie można znaleźć w książce Kazimierza Kuratowskiego "Pół wieku matematyki polskiej 1920-1970" wydanej przez Książkę i Wiedzę w 1973 roku
6 listopada 1936 roku Stanisław Mazur postawił pewien problem dotyczący analizy funkcjonalnej. Za jego rozwiązanie obiecał ofiarować żywą gęś. W 1972 roku w Warszawie gęś odebrał szwedzki matematyk Per Enflo...
Tytułowy problem, postawiony przez Stanisława Mazura, brzmi:
Problem. Czy dla każdej funkcji ciągłej 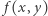 określonej w kwadracie
określonej w kwadracie 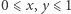 i dowolnej liczby dodatniej
i dowolnej liczby dodatniej  istnieją takie punkty kwadratu
istnieją takie punkty kwadratu 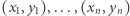 oraz liczby
oraz liczby 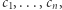 że dla wszystkich punktów
że dla wszystkich punktów 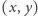 tego kwadratu
tego kwadratu
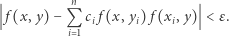 |
Problem nie wygląda szczególnie interesująco, ale Mazur wiedział, że ma on związek z ważnym wówczas pytaniem:
Problem. Czy każda ośrodkowa przestrzeń Banacha ma bazę Schaudera.
Baza Schaudera 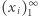 przestrzeni Banacha
przestrzeni Banacha 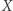 to taki ciąg jej punktów, że dowolny element
to taki ciąg jej punktów, że dowolny element 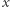 tej przestrzeni daje się przedstawić w postaci
tej przestrzeni daje się przedstawić w postaci 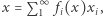 przy czym współczynniki
przy czym współczynniki 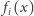 są funkcjonałami ciągłymi. Okazało się później (udowodnił to wielki matematyk francuski Alexander Grothendieck), że problem Mazura jest równoważny z problemem aproksymacji dla przestrzeni Banacha
są funkcjonałami ciągłymi. Okazało się później (udowodnił to wielki matematyk francuski Alexander Grothendieck), że problem Mazura jest równoważny z problemem aproksymacji dla przestrzeni Banacha 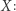
Problem. Czy każdy liniowy operator zwarty z dowolnej przestrzeni Banacha do 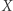 daje się aproksymować w normie przez operatory skończenie wymiarowe?
daje się aproksymować w normie przez operatory skończenie wymiarowe?
Jest tak, jeśli przestrzeń 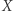 ma bazę Schaudera. Za rozwiązanie tego problemu Stanisław Mazur obiecał ufundować nagrodę w postaci żywej gęsi. Rozwiązał go po wielu latach Per Enflo w pracy opublikowanej w roku 1973. Odpowiedź była negatywna: Enflo skonstruował przestrzeń bez własności aproksymacji, a tym samym bez bazy Schaudera. Wynik ten wywołał sensację; gdy było już pewne, że jest poprawny, Enflo został zaproszony do Warszawy po odbiór nagrody.
ma bazę Schaudera. Za rozwiązanie tego problemu Stanisław Mazur obiecał ufundować nagrodę w postaci żywej gęsi. Rozwiązał go po wielu latach Per Enflo w pracy opublikowanej w roku 1973. Odpowiedź była negatywna: Enflo skonstruował przestrzeń bez własności aproksymacji, a tym samym bez bazy Schaudera. Wynik ten wywołał sensację; gdy było już pewne, że jest poprawny, Enflo został zaproszony do Warszawy po odbiór nagrody.
Prezydent Uniwersytetu Kalifornijskiego w Berkeley, gdzie Enflo wówczas pracował, ofiarował mu bilet na przelot. Ponieważ wydarzenie miało miejsce w grudniu 1972 roku, na kilka dni przed Bożym Narodzeniem, szczęśliwy matematyk przy okazji mógł odwiedzić rodzinę w Szwecji. Sławetną gęś zakupiła i umieściła w koszyku dr Anna Warzecha. Enflo otrzymał ją w prywatnym mieszkaniu Mazura (nie byłem przy tym obecny). Słynne zdjęcie Mazura, Enflo i gęsi zrobił wtedy Wiesław Szlenk. Tego dnia gość wygłosił wykład podczas zebrania Towarzystwa Matematycznego w Pałacu Kultury i Nauki (Mazur nie był obecny na tym wykładzie). Reporter TVP (niejaki "Wicherek") nagrywał tylko początek sesji, więc gdy gęś była już w piecu, można ją było zobaczyć żywą w wieczornych wiadomościach telewizyjnych.
Po wykładzie powstał naturalny problem, co zrobić z gęsią. Enflo następnego dnia miał lecieć do Sztokholmu i nie mógł zabrać jej w żadnej postaci. Problem rozwiązała moja żona Hania. Obiecała upiec gęś pod warunkiem, że ktoś ją zabije i oskubie. Egzekucji dokonał Przemek Wojtaszczyk, obecnie profesor, a wtedy doktorant Aleksandra Pełczyńskiego, który polecił mu to uczynić. Z podobnych powodów gęś została oskubana i oczyszczona przez moją doktorantkę Ewę Ligocką (obecnie emerytowaną profesor UW i laureatkę nagrody Bergmana w USA). Pióra latały po całym domu. Upieczona gęś została podana około trzeciej nad ranem. Przedtem goście dostali coś do jedzenia i picia, a Enflo przez cały czas grał na pianinie. Był i jest doskonałym pianistą, między innymi zagrał sonatę E-dur Beethovena (opus 109). Powiedział mi kiedyś, że dwukrotnie brał udział w międzynarodowych konkursach pianistycznych, i że pewnego razu zaproszono go na konferencję matematyczną, ale nie po to, aby coś powiedział, ale po to, aby zagrał. Było mu co prawda smutno, ale się zgodził. Pamiętam, że kiedyś podczas wizyty w Kent (Ohio, USA) byłem wraz z żoną zaproszony do Państwa Enflo na kolację. Na początku był koncert: pani Enflo zaśpiewała arię z 208. kantaty Bacha (była śpiewaczką w operze w Cleveland), a Per jej akompaniował. Potem słuchaliśmy Chopina, a w tym czasie pani Enflo szykowała kolację. Kilka dni później byliśmy na publicznym koncercie, na którym oboje wykonywali pieśni Schuberta. Słyszałem, że Per nadal koncertuje, czasami nawet z orkiestrą.
Per Enflo miał także swój udział w rozwiązaniu innego słynnego, i chyba ważniejszego, problemu, mianowicie problemu podprzestrzeni niezmienniczej. Było to pytanie
Problem. Czy każdy operator liniowy ciągły 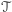 przestrzeni Banacha
przestrzeni Banacha 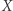 w siebie ma właściwą podprzestrzeń niezmienniczą, to znaczy taką podprzestrzeń domkniętą
w siebie ma właściwą podprzestrzeń niezmienniczą, to znaczy taką podprzestrzeń domkniętą 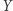 przestrzeni
przestrzeni 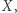 że
że 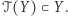
Per pokazał mi kiedyś gruby całkowicie zapisany brulion z konstrukcją kontrprzykładu. Zapamiętałem tylko, że na którejś stronie był sformułowany lemat 68. (numer zmyślony) z uwagą, że dowód jest podobny do dowodu lematu 36. Praca była oddana do druku, ale nikt nie był w stanie tego przeczytać. Słyszałem, że została opublikowana dopiero wtedy, gdy na ten sam temat ukazała się praca Charlesa Reada ze znacznie prostszą konstrukcją, mieszczącą się na kilkunastu stronach. Swoją drogą Charles Read był także niezłym pianistą. Zagrał u mnie w domu sonatę h-moll Liszta na tym samym pianinie, na którym grał Enflo. Pianino jest więc mocno związane z problemem podprzestrzeni niezmienniczej. Piszę dużo o muzyce ze względu na pewną klasyfikację matematyków: na takich, którzy chodzą po górach, grają w szachy lub słuchają muzyki. Istnieją co prawda wybitni matematycy nie podlegający tej klasyfikacji, ale jest ich stosunkowo niewielu.