Klub 44M - zadania IV 2018»Zadanie 760
o zadaniu...
- Zadanie pochodzi z artykułu Klub 44M - zadania IV 2018
- Publikacja w Delcie: kwiecień 2018
- Publikacja elektroniczna: 29 marca 2018
- Artykuł źródłowy w wersji do druku [application/pdf]: (68 KB)
-
Zadanie 760 zaproponował pan Paweł Kubit z Krakowa.
Dowieść, że istnieje nieskończenie wiele dodatnich liczb rzeczywistych 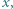 dla których każda z liczb
dla których każda z liczb 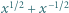 oraz
oraz 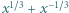 jest całkowita.
jest całkowita.


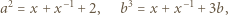
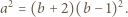
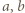 są naturalne, czynnik
są naturalne, czynnik 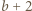 musi być kwadratem liczby naturalnej; więc
musi być kwadratem liczby naturalnej; więc 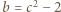
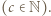 Zgodnie z (1), jest to suma liczb
Zgodnie z (1), jest to suma liczb 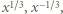 których iloczyn wynosi 1. Zatem
których iloczyn wynosi 1. Zatem 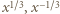 to pierwiastki trójmianu kwadratowego
to pierwiastki trójmianu kwadratowego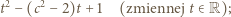
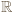 ) gdy
) gdy 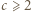 ; i są wówczas dodatnie. Wyznaczamy je zwykłą metodą, podnosimy do trzeciej potęgi, i dostajemy wniosek:
; i są wówczas dodatnie. Wyznaczamy je zwykłą metodą, podnosimy do trzeciej potęgi, i dostajemy wniosek: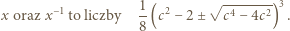
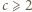 określamy wzorami (4) parę liczb rzeczywistych, wzajemnie odwrotnych:
określamy wzorami (4) parę liczb rzeczywistych, wzajemnie odwrotnych:  oraz
oraz 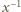 (jedna ze znakiem plus w nawiasie, druga ze znakiem minus). Wówczas
(jedna ze znakiem plus w nawiasie, druga ze znakiem minus). Wówczas 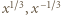 są pierwiastkami trójmianu (3); ich suma wynosi
są pierwiastkami trójmianu (3); ich suma wynosi 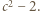 Liczby
Liczby 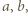 zdefiniowane wzorami (1), spełniają równość (2); a ponieważ
zdefiniowane wzorami (1), spełniają równość (2); a ponieważ 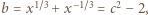 zatem prawa strona wzoru (2) jest kwadratem liczby całkowitej, więc liczba
zatem prawa strona wzoru (2) jest kwadratem liczby całkowitej, więc liczba 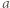 jest całkowita (liczba
jest całkowita (liczba 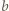 oczywiście też).
oczywiście też).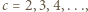 przedstawia ogólną postać liczb
przedstawia ogólną postać liczb 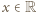 o rozważanej w zadaniu własności.
o rozważanej w zadaniu własności.