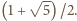Klub 44M - zadania IV 2015»Zadanie 699
o zadaniu...
- Zadanie pochodzi z artykułu Klub 44M - zadania IV 2015
- Publikacja w Delcie: kwiecień 2015
- Publikacja elektroniczna: 31 marca 2015
- Artykuł źródłowy w wersji do druku [application/pdf]: (58 KB)
Cztery różne punkty na płaszczyźnie wyznaczają sześć odcinków. Załóżmy, że trzy spośród tych odcinków mają jednakową długość 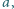 zaś pozostałe trzy mają jednakową długość
zaś pozostałe trzy mają jednakową długość 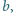 przy czym
przy czym 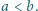 Wyznaczyć wszystkie możliwe wartości stosunku
Wyznaczyć wszystkie możliwe wartości stosunku 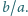

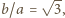 i jest to jedna z możliwych wartości rozpatrywanego stosunku. Dalej przyjmijmy, że nie pojawia się trójkąt równoboczny. Trzy odcinki długości
i jest to jedna z możliwych wartości rozpatrywanego stosunku. Dalej przyjmijmy, że nie pojawia się trójkąt równoboczny. Trzy odcinki długości 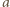 tworzą wówczas łamaną (nie zamkniętą), i tak samo trzy odcinki długości
tworzą wówczas łamaną (nie zamkniętą), i tak samo trzy odcinki długości 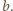 Można tak ustalić oznaczenia
Można tak ustalić oznaczenia 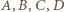 danych punktów, by
danych punktów, by
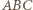 podstawa
podstawa 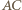 jest dłuższa niż ramiona. W trójkącie równoramiennym
jest dłuższa niż ramiona. W trójkącie równoramiennym 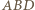 podstawa
podstawa 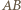 jest krótsza niż ramiona. Zatem
jest krótsza niż ramiona. Zatem 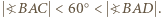
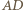 jest wspólnym bokiem przystających trójkątów równoramiennych
jest wspólnym bokiem przystających trójkątów równoramiennych 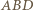 oraz
oraz 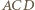 (o podstawach
(o podstawach 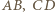 ). Te trójkąty muszą być położone symetrycznie - albo względem środka odcinka
). Te trójkąty muszą być położone symetrycznie - albo względem środka odcinka 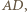 albo względem symetralnej tego odcinka. W pierwszym z tych przypadków powstałby równoległobok
albo względem symetralnej tego odcinka. W pierwszym z tych przypadków powstałby równoległobok 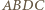 ; to jednak nie jest możliwe, skoro kąt
; to jednak nie jest możliwe, skoro kąt 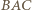 jest mniejszy od kąta
jest mniejszy od kąta 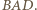
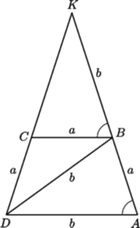
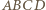 o podstawach
o podstawach 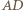 (dłuższej) i
(dłuższej) i 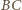 (krótszej). Półproste
(krótszej). Półproste 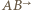 i
i 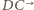 przecinają się w punkcie, który nazwiemy
przecinają się w punkcie, który nazwiemy 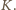 Trójkąty równoramienne
Trójkąty równoramienne 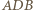 i
i 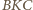 mają równe podstawy
mają równe podstawy 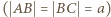 i równe kąty przy podstawie
i równe kąty przy podstawie 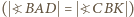 - są więc przystające. Stąd
- są więc przystające. Stąd 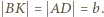 Trójkąt
Trójkąt 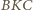 jest ponadto podobny do
jest ponadto podobny do 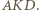 Otrzymujemy proporcję
Otrzymujemy proporcję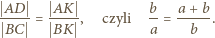
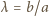 spełnia zatem równanie
spełnia zatem równanie 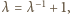 którego jedynym dodatnim pierwiastkiem jest
którego jedynym dodatnim pierwiastkiem jest 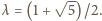 Realizację tej wartości uzyskujemy, biorąc jako
Realizację tej wartości uzyskujemy, biorąc jako 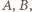
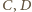 cztery wierzchołki pięciokąta foremnego.
cztery wierzchołki pięciokąta foremnego.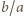 są liczby
są liczby 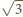 oraz
oraz