Ekstrema»Zadanie 1
Koledzy Fredka mieszkają na okręgu. Fredek chce ich wszystkich odwiedzić i u każdego z nich zatankować (bak w samochodzie Fredka ma nieograniczoną pojemność). Kiedy zatankowane paliwo zużyje się całkowicie, Fredek nie będzie miał możliwości kontynuowania podróży. Wszyscy koledzy Fredka mają w sumie dokładnie tyle paliwa, ile potrzeba Fredkowi na odbycie podróży po całym okręgu. Udowodnij, że Fredek może rozpocząć podróż od takiego kolegi, że jadąc zegarowo po okręgu i tankując po drodze, odwiedzi wszystkich kolegów i wróci do punktu wyjścia.
kolegów podróż jest możliwa
i rozważmy
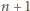kolegów. Ponumerujmy ich zegarowo wokół okręgu:
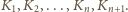
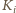ma tyle paliwa, by
wystarczyło na podróż do
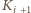(gdzie
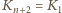). Gdyby bowiem
żaden kolega nie spełniał tego warunku, to łączna ilość posiadanego przez
wszystkich paliwa byłaby mniejsza, niż potrzeba do pełnego okrążenia,
sprzecznie z założeniem.
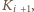wraz ze swoim paliwem, złożyłby wizytę koledze
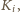to z założenia indukcyjnego Fredek mógłby odwiedzić wszystkich
(
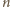punktów na okręgu).
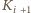gościł
u
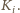Wiemy, że gdyby u
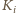zatankował całe paliwo oferowane
przez
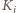i
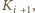to mógłby dokończyć podróż. U kolegi
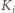dostanie wystarczająco wiele, by dotrzeć do
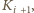bo tak
wybraliśmy
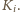Potem u
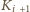zatankuje resztę paliwa
oferowanego przez tych dwóch kolegów, więc – jak już wiemy – dokończy
podróż.