Zmyślna tożsamość
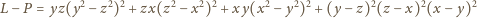
użyta w rozwiązaniu zaiste trywializuje problem, a jej sprawdzenie jest
czynnością czysto mechaniczną (Mathematica robi to w ułamku sekundy;
ręcznie sprawdzamy ją w parę minut). Ale jak na nią wpaść?!
Na przykład tak: dla
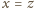 różnica
różnica
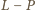 przyjmuje wartość
przyjmuje wartość
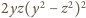 ; analogicznie dla
; analogicznie dla
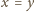 i dla
i dla
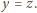 Zatem
przyjmując
Zatem
przyjmując
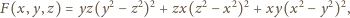
widzimy, że wielomian
 ma wartość zero, gdy dowolne
dwie zmienne są równe. Jest więc podzielny przez wielomian
ma wartość zero, gdy dowolne
dwie zmienne są równe. Jest więc podzielny przez wielomian
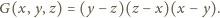
Skoro zaś
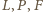 są wielomianami symetrycznymi, natomiast
są wielomianami symetrycznymi, natomiast
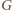 jest
wielomianem antysymetrycznym (zmienia znak przy transpozycji zmiennych),
wynika stąd, że iloraz
jest
wielomianem antysymetrycznym (zmienia znak przy transpozycji zmiennych),
wynika stąd, że iloraz
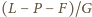 też jest antysymetryczny – ma
więc wartość zero, gdy dwie zmienne są równe, i w konsekwencji dzieli się
znów przez
też jest antysymetryczny – ma
więc wartość zero, gdy dwie zmienne są równe, i w konsekwencji dzieli się
znów przez
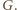 To znaczy, że wielomian
To znaczy, że wielomian
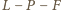 dzieli się przez
dzieli się przez
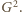 Są to wielomiany jednorodne szóstego stopnia, ich iloraz musi być
stałą.
Są to wielomiany jednorodne szóstego stopnia, ich iloraz musi być
stałą.
Wniosek:
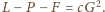 Wartość stałej
Wartość stałej
 znajdujemy,
podstawiając w miejsce
znajdujemy,
podstawiając w miejsce
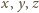 dowolne trzy różne liczby; wychodzi
dowolne trzy różne liczby; wychodzi
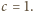 Tak więc
Tak więc
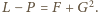 Jest to właśnie „ta zmyślna”
tożsamość.
Jest to właśnie „ta zmyślna”
tożsamość.
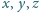 :
:
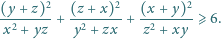

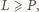 gdzie
gdzie
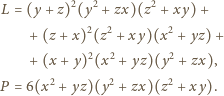
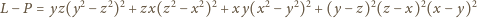
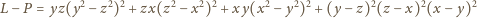
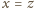 różnica
różnica
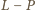 przyjmuje wartość
przyjmuje wartość
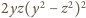 ; analogicznie dla
; analogicznie dla
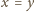 i dla
i dla
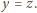 Zatem
przyjmując
Zatem
przyjmując
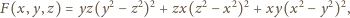
 ma wartość zero, gdy dowolne
dwie zmienne są równe. Jest więc podzielny przez wielomian
ma wartość zero, gdy dowolne
dwie zmienne są równe. Jest więc podzielny przez wielomian
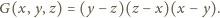
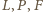 są wielomianami symetrycznymi, natomiast
są wielomianami symetrycznymi, natomiast
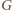 jest
wielomianem antysymetrycznym (zmienia znak przy transpozycji zmiennych),
wynika stąd, że iloraz
jest
wielomianem antysymetrycznym (zmienia znak przy transpozycji zmiennych),
wynika stąd, że iloraz
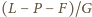 też jest antysymetryczny – ma
więc wartość zero, gdy dwie zmienne są równe, i w konsekwencji dzieli się
znów przez
też jest antysymetryczny – ma
więc wartość zero, gdy dwie zmienne są równe, i w konsekwencji dzieli się
znów przez
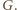 To znaczy, że wielomian
To znaczy, że wielomian
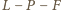 dzieli się przez
dzieli się przez
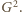 Są to wielomiany jednorodne szóstego stopnia, ich iloraz musi być
stałą.
Są to wielomiany jednorodne szóstego stopnia, ich iloraz musi być
stałą.
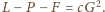 Wartość stałej
Wartość stałej
 znajdujemy,
podstawiając w miejsce
znajdujemy,
podstawiając w miejsce
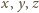 dowolne trzy różne liczby; wychodzi
dowolne trzy różne liczby; wychodzi
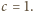 Tak więc
Tak więc
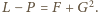 Jest to właśnie „ta zmyślna”
tożsamość.
Jest to właśnie „ta zmyślna”
tożsamość.