Klub 44M - zadania III 2017»Zadanie 738
o zadaniu...
- Zadanie pochodzi z artykułu Klub 44M - zadania III 2017
- Publikacja w Delcie: marzec 2017
- Publikacja elektroniczna: 1 marca 2017
- Artykuł źródłowy w wersji do druku [application/pdf]: (67 KB)
-
Zadanie 738 zaproponował pan Bartłomiej Pawlik z Limanowej.
Wypisując, jedna za drugą, wszystkie liczby całkowite dodatnie, mające (w systemie dziesiętnym) co najwyżej 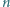 cyfr, piszemy łącznie
cyfr, piszemy łącznie 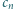 cyfr (np.
cyfr (np. 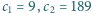 ); w tym
); w tym 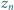 zer (np.
zer (np. 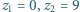 ). Czy równość
). Czy równość 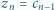 jest spełniona dla wszystkich liczb naturalnych
jest spełniona dla wszystkich liczb naturalnych 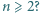

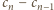 to liczba cyfr użytych do zapisania wszystkich liczb
to liczba cyfr użytych do zapisania wszystkich liczb  -cyfrowych. Jest tych liczb
-cyfrowych. Jest tych liczb 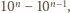 czyli
czyli 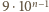 ; zatem
; zatem 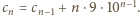 W zapisie każdej z nich cyfra wiodąca jest różna od zera; po jej odrzuceniu, pozostała część zapisu to dowolny ciąg długości
W zapisie każdej z nich cyfra wiodąca jest różna od zera; po jej odrzuceniu, pozostała część zapisu to dowolny ciąg długości 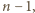 złożony z dowolnych cyfr (formalnie - słowo z alfabetu 10-elementowego).
złożony z dowolnych cyfr (formalnie - słowo z alfabetu 10-elementowego).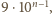 jest w nich więc
jest w nich więc 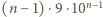 cyfr, a wszystkie cyfry są równouprawnione. Dziesiąta część spośród nich to zera. To znaczy, że w zapisie wszystkich liczb
cyfr, a wszystkie cyfry są równouprawnione. Dziesiąta część spośród nich to zera. To znaczy, że w zapisie wszystkich liczb 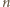 -cyfrowych mamy
-cyfrowych mamy 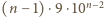 zer. Tak więc
zer. Tak więc 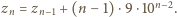 Pisząc
Pisząc 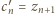 widzimy, że ciągi
widzimy, że ciągi 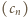 i
i 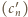 spełniają identyczną zależność rekurencyjną. Ponieważ
spełniają identyczną zależność rekurencyjną. Ponieważ 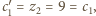 wynika stąd, że
wynika stąd, że 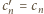 (dla
(dla 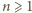 ), czyli
), czyli 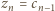 (dla
(dla 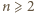 ).
).