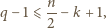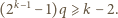Zapiszmy liczbę 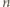 w postaci
w postaci 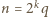 (
( 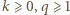 całkowite,
całkowite, 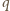 nieparzyste). Znajdujemy wykładnik
nieparzyste). Znajdujemy wykładnik 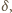 dla którego
dla którego
 |
(1) |
Jeśli pewien wykładnik spełnia ten warunek, to jego dwukrotność też. Można więc wybrać 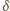 tak, by
tak, by
 |
(2) |
Liczbę 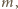 o jaką pyta zadanie, spróbujemy znaleźć wśród liczb postaci
o jaką pyta zadanie, spróbujemy znaleźć wśród liczb postaci 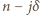 (
( 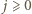 całkowite). Dla
całkowite). Dla 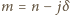 różnica
różnica
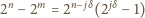
będzie podzielna przez 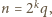 jeśli tylko
jeśli tylko 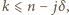 bowiem czynnik w nawiasie dzieli się przez
bowiem czynnik w nawiasie dzieli się przez 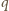 (por. (1)). Biorąc jeszcze pod uwagę wymaganie, by
(por. (1)). Biorąc jeszcze pod uwagę wymaganie, by 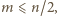 widzimy, że wystarczy znaleźć liczbę
widzimy, że wystarczy znaleźć liczbę 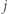 spełniającą nierówność
spełniającą nierówność
 |
(3) |
wówczas liczba 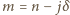 spełni wszystkie żądane warunki.
spełni wszystkie żądane warunki.
Gdy  jest liczbą nieparzystą, czyli gdy
jest liczbą nieparzystą, czyli gdy 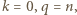 można wziąć
można wziąć 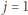 (por. (2)).
(por. (2)).
Gdy  jest liczbą parzystą (więc
jest liczbą parzystą (więc 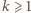 ), warunki (3) postulują istnienie wielokrotności liczby
), warunki (3) postulują istnienie wielokrotności liczby 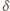 w przedziale
w przedziale ![[n/2,n− k].](/math/temat/matematyka/teoria_liczb/zadania/2016/09/01/zm-k44-726/4x-4209685659c448dfca3440cc75c1cd5715973512-im-66,57,43-FF,FF,FF.gif) Do tego wystarcza, by
Do tego wystarcza, by 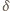 nie przekraczała wartości
nie przekraczała wartości 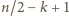 (bo tyle jest liczb całkowitych w tym przedziale); a dzięki oszacowaniu (2) wystarczy, by zachodziła nierówność
(bo tyle jest liczb całkowitych w tym przedziale); a dzięki oszacowaniu (2) wystarczy, by zachodziła nierówność
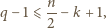
czyli (równoważnie)
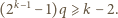
To kończy rozwiązanie, bowiem ostatnia nierówność jest słuszna dla każdej pary liczb całkowitych 
 będzie ustaloną liczbą całkowitą dodatnią. Dowieść, że istnieje nieujemna liczba całkowita
będzie ustaloną liczbą całkowitą dodatnią. Dowieść, że istnieje nieujemna liczba całkowita 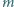 taka, że
taka, że 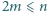 oraz różnica
oraz różnica 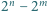 dzieli się przez
dzieli się przez 

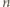 w postaci
w postaci 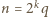 (
( 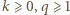 całkowite,
całkowite, 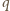 nieparzyste). Znajdujemy wykładnik
nieparzyste). Znajdujemy wykładnik 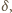 dla którego
dla którego
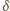 tak, by
tak, by
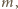 o jaką pyta zadanie, spróbujemy znaleźć wśród liczb postaci
o jaką pyta zadanie, spróbujemy znaleźć wśród liczb postaci 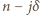 (
( 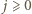 całkowite). Dla
całkowite). Dla 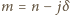 różnica
różnica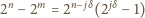
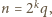 jeśli tylko
jeśli tylko 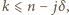 bowiem czynnik w nawiasie dzieli się przez
bowiem czynnik w nawiasie dzieli się przez 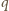 (por. (1)). Biorąc jeszcze pod uwagę wymaganie, by
(por. (1)). Biorąc jeszcze pod uwagę wymaganie, by 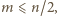 widzimy, że wystarczy znaleźć liczbę
widzimy, że wystarczy znaleźć liczbę  spełniającą nierówność
spełniającą nierówność
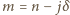 spełni wszystkie żądane warunki.
spełni wszystkie żądane warunki. jest liczbą nieparzystą, czyli gdy
jest liczbą nieparzystą, czyli gdy 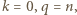 można wziąć
można wziąć 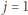 (por. (2)).
(por. (2)). jest liczbą parzystą (więc
jest liczbą parzystą (więc 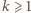 ), warunki (3) postulują istnienie wielokrotności liczby
), warunki (3) postulują istnienie wielokrotności liczby 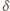 w przedziale
w przedziale ![[n/2,n− k].](/math/temat/matematyka/teoria_liczb/zadania/2016/09/01/zm-k44-726/4x-4209685659c448dfca3440cc75c1cd5715973512-im-66,57,43-FF,FF,FF.gif) Do tego wystarcza, by
Do tego wystarcza, by 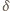 nie przekraczała wartości
nie przekraczała wartości 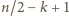 (bo tyle jest liczb całkowitych w tym przedziale); a dzięki oszacowaniu (2) wystarczy, by zachodziła nierówność
(bo tyle jest liczb całkowitych w tym przedziale); a dzięki oszacowaniu (2) wystarczy, by zachodziła nierówność