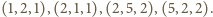Klub 44M - zadania V 2016»Zadanie 722
o zadaniu...
- Zadanie pochodzi z artykułu Klub 44M - zadania V 2016
- Publikacja w Delcie: maj 2016
- Publikacja elektroniczna: 1 maja 2016
- Artykuł źródłowy w wersji do druku [application/pdf]: (106 KB)
-
Zadanie 722 zaproponował pan Witold Bednarek z Łodzi.
Rozwiązać równanie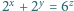 
w liczbach całkowitych dodatnich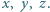 
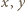nie mogą być równe, gdyż wówczas lewa strona równania byłaby potęgą dwójki. Przyjmijmy więc, że 
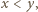i zapiszmy 
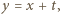gdzie 
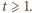Równanie przybiera postać 
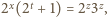z której wynika, że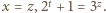 
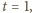to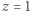 
; dostajemy rozwiązanie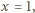 
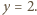
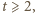to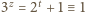 
(mod 4), skąd wniosek, że 
jest liczbą parzystą: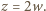 
Dostajemy równanie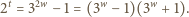
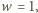czyli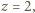 
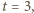co daje rozwiązanie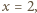 
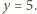
i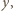 
widzimy, że równanie ma cztery rozwiązania 
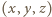w liczbach całkowitych dodatnich: 