Klub 44M - zadania III 2016»Zadanie 718
o zadaniu...
- Zadanie pochodzi z artykułu Klub 44M - zadania III 2016
- Publikacja w Delcie: marzec 2016
- Publikacja elektroniczna: 29 lutego 2016
- Artykuł źródłowy w wersji do druku [application/pdf]: (84 KB)
-
Zadanie 718 zaproponował pan Tomasz Ordowski.
Dowieść, że dla dowolnych dodatnich liczb całkowitych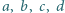 
zachodzi równość
![[a, b,c,d] =-a⋅b-⋅c⋅d- ⋅--(a,-b,c)⋅(a,b,d)-⋅(a,c,d)-⋅(b,c,d)---. (a, b,c,d) (a,b) ⋅(a,c)⋅(a,d) ⋅(b,c) ⋅(b,d) ⋅(c,d)](/math/temat/matematyka/teoria_liczb/zadania/2016/02/29/zm-k44-718/2x-f64cd4667e200cae0b647d7a1c3170835ae3432d-dm-2C,6B,73-FF,FF,FF.gif)
Nawias kwadratowy oznacza najmniejszą wspólną wielokrotność, zaś nawias okrągły - największy wspólny dzielnik liczb ujętych w ów nawias.
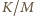(licznik 
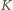to iloczyn ośmiu czynników, mianownik 
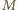to iloczyn siedmiu czynników). Lewa strona to ![|L = [a,b,c,d].](/math/temat/matematyka/teoria_liczb/zadania/2016/02/29/zm-k44-718/4x-3ae01d082f06ba518fa4af60a10f4ff5720e5299-im-66,57,43-FF,FF,FF.gif)
Wystarczy pokazać, że dowolna liczba pierwsza wchodzi do rozkładów liczb 
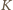oraz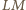 
w jednakowej potędze (być może zerowej).
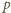i przyjmijmy, że liczby 
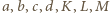są podzielne odpowiednio przez 
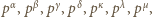ale nie przez 
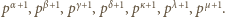Wówczas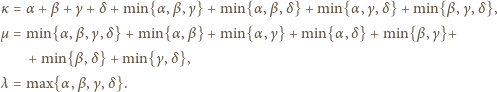
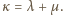
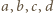) nie tracimy ogólności zakładając, że 
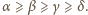Napisane równości uzyskują postać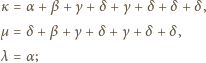
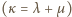gotowa.