Można przyjąć, że 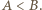 Wskażemy indukcyjną konstrukcję ciągu zbiorów
Wskażemy indukcyjną konstrukcję ciągu zbiorów 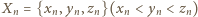 o wymaganych własnościach. Zaczniemy od trójki
o wymaganych własnościach. Zaczniemy od trójki 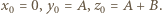 Załóżmy, że zbiory
Załóżmy, że zbiory 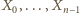 zostały już określone. Wówczas definiujemy
zostały już określone. Wówczas definiujemy 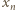 jako najmniejszą liczbę naturalną jeszcze niewykorzystaną (tzn. nieobecną w zbiorze
jako najmniejszą liczbę naturalną jeszcze niewykorzystaną (tzn. nieobecną w zbiorze 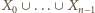 ) - to już gwarantuje, że w wyniku całej konstrukcji wszystkie liczby naturalne zostaną użyte oraz że ciąg
) - to już gwarantuje, że w wyniku całej konstrukcji wszystkie liczby naturalne zostaną użyte oraz że ciąg 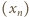 będzie rosnący.
będzie rosnący.
Aby dokończyć określenie zbioru 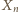 (gdy
(gdy 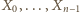 już mamy), patrzymy na liczbę
już mamy), patrzymy na liczbę 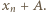 Jeżeli jest ona jeszcze niewykorzystana, przyjmujemy ją jako
Jeżeli jest ona jeszcze niewykorzystana, przyjmujemy ją jako 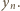 Jeżeli jest wykorzystana, bierzemy jako
Jeżeli jest wykorzystana, bierzemy jako 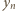 liczbę
liczbę 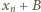 ; i z konieczności przyjmujemy
; i z konieczności przyjmujemy 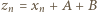 (tak więc jedna z różnic
(tak więc jedna z różnic 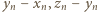 będzie równa
będzie równa 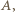 a druga
a druga 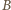 ). Tak określona liczba
). Tak określona liczba 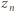 jest większa od liczb
jest większa od liczb 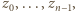 więc nie została wcześniej wykorzystana.
więc nie została wcześniej wykorzystana.
Pozostaje uzasadnić, że w przypadku, gdy liczba 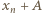 została już wykorzystana, wówczas liczba
została już wykorzystana, wówczas liczba 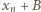 pozostała niewykorzystana (i może być użyta jako
pozostała niewykorzystana (i może być użyta jako 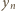 ). Przypuśćmy, że liczba
). Przypuśćmy, że liczba 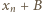 znalazła się w którymś zbiorze
znalazła się w którymś zbiorze 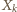 o numerze
o numerze 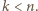 Skoro
Skoro 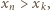 to
to 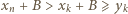 ; musiałaby zajść równość
; musiałaby zajść równość 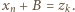 Ale
Ale 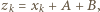 więc mielibyśmy
więc mielibyśmy 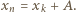 Liczba
Liczba 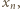 niewykorzystana aż do
niewykorzystana aż do 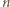 -tego kroku konstrukcji, tym bardziej nie była jeszcze wykorzystana w momencie konstrukcji zbioru
-tego kroku konstrukcji, tym bardziej nie była jeszcze wykorzystana w momencie konstrukcji zbioru 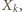 więc na mocy przyjętego algorytmu powinna była zostać użyta jako
więc na mocy przyjętego algorytmu powinna była zostać użyta jako 
Uzyskana sprzeczność dowodzi niesłuszności przypuszczenia, że 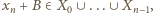 i uzasadnia poprawność określenia
i uzasadnia poprawność określenia 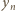 ; powstały zbiór
; powstały zbiór 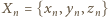 jest rozłączny ze zbiorami
jest rozłączny ze zbiorami 
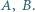 Wykazać, że zbiór wszystkich liczb całkowitych nieujemnych może być przedstawiony jako suma rozłącznych zbiorów trójelementowych, przy czym w każdym z tych zbiorów liczba środkowa (co do wielkości) różni się od jednej z dwóch pozostałych liczb o
Wykazać, że zbiór wszystkich liczb całkowitych nieujemnych może być przedstawiony jako suma rozłącznych zbiorów trójelementowych, przy czym w każdym z tych zbiorów liczba środkowa (co do wielkości) różni się od jednej z dwóch pozostałych liczb o 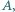 zaś od drugiej o
zaś od drugiej o 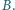

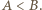 Wskażemy indukcyjną konstrukcję ciągu zbiorów
Wskażemy indukcyjną konstrukcję ciągu zbiorów 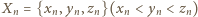 o wymaganych własnościach. Zaczniemy od trójki
o wymaganych własnościach. Zaczniemy od trójki 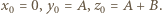 Załóżmy, że zbiory
Załóżmy, że zbiory 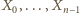 zostały już określone. Wówczas definiujemy
zostały już określone. Wówczas definiujemy 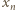 jako najmniejszą liczbę naturalną jeszcze niewykorzystaną (tzn. nieobecną w zbiorze
jako najmniejszą liczbę naturalną jeszcze niewykorzystaną (tzn. nieobecną w zbiorze 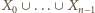 ) - to już gwarantuje, że w wyniku całej konstrukcji wszystkie liczby naturalne zostaną użyte oraz że ciąg
) - to już gwarantuje, że w wyniku całej konstrukcji wszystkie liczby naturalne zostaną użyte oraz że ciąg 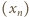 będzie rosnący.
będzie rosnący.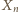 (gdy
(gdy 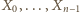 już mamy), patrzymy na liczbę
już mamy), patrzymy na liczbę 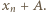 Jeżeli jest ona jeszcze niewykorzystana, przyjmujemy ją jako
Jeżeli jest ona jeszcze niewykorzystana, przyjmujemy ją jako 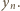 Jeżeli jest wykorzystana, bierzemy jako
Jeżeli jest wykorzystana, bierzemy jako 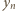 liczbę
liczbę 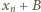 ; i z konieczności przyjmujemy
; i z konieczności przyjmujemy 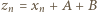 (tak więc jedna z różnic
(tak więc jedna z różnic 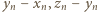 będzie równa
będzie równa 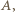 a druga
a druga 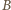 ). Tak określona liczba
). Tak określona liczba 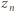 jest większa od liczb
jest większa od liczb 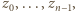 więc nie została wcześniej wykorzystana.
więc nie została wcześniej wykorzystana.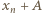 została już wykorzystana, wówczas liczba
została już wykorzystana, wówczas liczba 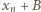 pozostała niewykorzystana (i może być użyta jako
pozostała niewykorzystana (i może być użyta jako 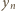 ). Przypuśćmy, że liczba
). Przypuśćmy, że liczba 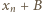 znalazła się w którymś zbiorze
znalazła się w którymś zbiorze 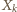 o numerze
o numerze 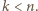 Skoro
Skoro 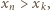 to
to 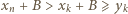 ; musiałaby zajść równość
; musiałaby zajść równość 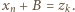 Ale
Ale 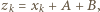 więc mielibyśmy
więc mielibyśmy 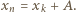 Liczba
Liczba 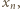 niewykorzystana aż do
niewykorzystana aż do 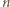 -tego kroku konstrukcji, tym bardziej nie była jeszcze wykorzystana w momencie konstrukcji zbioru
-tego kroku konstrukcji, tym bardziej nie była jeszcze wykorzystana w momencie konstrukcji zbioru 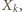 więc na mocy przyjętego algorytmu powinna była zostać użyta jako
więc na mocy przyjętego algorytmu powinna była zostać użyta jako 
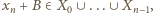 i uzasadnia poprawność określenia
i uzasadnia poprawność określenia 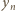 ; powstały zbiór
; powstały zbiór 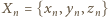 jest rozłączny ze zbiorami
jest rozłączny ze zbiorami 