Klub 44M - zadania I 2016»Zadanie 714
o zadaniu...
- Zadanie pochodzi z artykułu Klub 44M - zadania I 2016
- Publikacja w Delcie: styczeń 2016
- Publikacja elektroniczna: 1 stycznia 2016
- Artykuł źródłowy w wersji do druku [application/pdf]: (58 KB)
-
Zadanie 714 zaproponował pan Witold Bednarek z Łodzi.
Niech 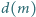 oznacza liczbę dodatnich dzielników liczby naturalnej
oznacza liczbę dodatnich dzielników liczby naturalnej 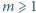
- (a)
- Wykazać, że istnieje nieskończenie wiele par różnych liczb naturalnych
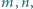 spełniających równanie
spełniających równanie 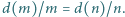
- (b)
- Czy istnieje para liczb naturalnych względnie pierwszych
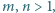 spełniających równanie
spełniających równanie 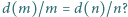

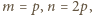 gdzie
gdzie 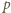 jest nieparzystą liczbą pierwszą, ma wymaganą własność, bowiem
jest nieparzystą liczbą pierwszą, ma wymaganą własność, bowiem 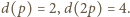
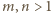 spełnia podane równanie:
spełnia podane równanie: 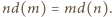 Skoro liczby
Skoro liczby 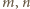 są względnie pierwsze, wynika stąd, że
są względnie pierwsze, wynika stąd, że  jest dzielnikiem liczby
jest dzielnikiem liczby 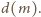 Wobec tego
Wobec tego 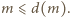 Taka nierówność zajść może (w formie równości) tylko wtedy, gdy każda liczba ze zbioru
Taka nierówność zajść może (w formie równości) tylko wtedy, gdy każda liczba ze zbioru 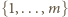 jest dzielnikiem liczby
jest dzielnikiem liczby  W szczególności
W szczególności  musi dzielić się przez
musi dzielić się przez 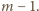 To zaś ma miejsce jedynie dla
To zaś ma miejsce jedynie dla 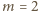 (rozważamy, z założenia, tylko
(rozważamy, z założenia, tylko 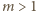 ).
).
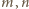 są symetryczne; to samo rozumowanie pokazuje, że także
są symetryczne; to samo rozumowanie pokazuje, że także 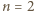 ; sprzeczność z założeniem, że
; sprzeczność z założeniem, że 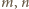 są względnie pierwsze. Nie istnieje więc para, o jakiej mowa w pytaniu (b).
są względnie pierwsze. Nie istnieje więc para, o jakiej mowa w pytaniu (b).