Klub 44M - zadania V 2015»Zadanie 701
o zadaniu...
- Zadanie pochodzi z artykułu Klub 44M - zadania V 2015
- Publikacja w Delcie: maj 2015
- Publikacja elektroniczna: 30 kwietnia 2015
- Artykuł źródłowy w wersji do druku [application/pdf]: (76 KB)
Niech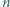 
będzie ustaloną dodatnią liczbą nieparzystą. Wyznaczyć największą możliwą liczność zbioru złożonego z liczb całkowitych dodatnich, mniejszych od 
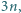w którym każde dwa różne elementy mają i różnicę, i sumę różną od 
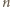jest nieparzysta, zatem zbiór wszystkich liczb parzystych, mniejszych od 
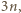ma własność, o którą chodzi. Jest ich 
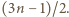Wykażemy, że jest to największa możliwa liczność.
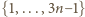na rozłączne pary: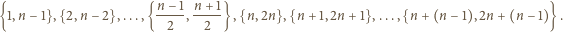
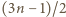par liczb. Zbiór o większej liczności (zawarty w 
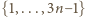) musi zawierać jedną z wymienionych par. Ale w każdej parze albo suma, albo różnica elementów jest równa 
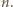Stąd nasza teza.