Niech będzie dowolną liczbą co najmniej dwucyfrową, której ostatnią cyfrą jest zero, a przedostatnią cyfrą nie jest dziewiątka. Wówczas w ciągu dwudziestu kolejnych liczb 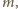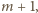…, 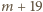znajduje się liczba o sumie cyfr podzielnej przez 11; jeśli bowiem suma cyfr liczby wynosi 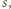to sumy cyfr liczb 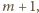…, 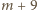wynoszą 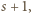…, 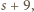zaś liczba 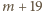ma sumę cyfr równą 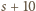; rzecz jasna, któraś z wartości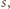 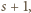…, 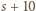dzieli się przez 11.

Pozostaje teraz zauważyć, że każdy ciąg kolejnych 39 liczb naturalnych zawiera 20-wyrazowy blok o wyrazie początkowym postaci, jak wyżej.