Zadanie zaproponował najstarszy stażem ligowiec Witold Bednarek – całe
szczęście, że wraz z rozwiązaniem. Oto ono:
Przypuśćmy, że dla pewnej liczby pierwszej
 liczba
liczba
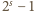 ma co
najmniej trzy różne dzielniki pierwsze
ma co
najmniej trzy różne dzielniki pierwsze
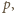
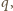
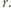 Wykażemy,
że wówczas trójka
Wykażemy,
że wówczas trójka
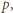
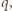
 spełnia postulowane
warunki.
spełnia postulowane
warunki.
Niech
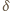 będzie najmniejszym wykładnikiem naturalnym, większym
od 1, dla którego
będzie najmniejszym wykładnikiem naturalnym, większym
od 1, dla którego
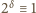 (mod
(mod
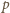 ). Z założenia także
). Z założenia także
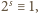 więc
więc
 dzieli się przez
dzieli się przez
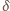 ; a skoro
; a skoro
 jest
liczbą pierwszą, to
jest
liczbą pierwszą, to
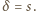 W myśl małego twierdzenia Fermata
W myśl małego twierdzenia Fermata
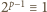 (mod
(mod
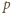 ), zatem
), zatem
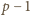 dzieli się przez
dzieli się przez
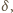 czyli
przez
czyli
przez
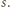
Analogicznie stwierdzamy, że
 jest dzielnikiem liczb
jest dzielnikiem liczb
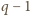 oraz
oraz
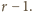 Podnosząc kongruencję
Podnosząc kongruencję
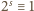 (mod
(mod
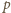 ) do potęgi
) do potęgi
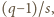 widzimy, że
widzimy, że
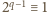 (mod
(mod
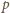 ). Tak samo,
cyklicznie,
). Tak samo,
cyklicznie,
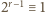 (mod
(mod
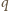 ),
),
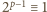 (mod
(mod
 ), czyli
mamy to, o co chodzi (a nawet więcej: okazuje się, że każda z liczb
), czyli
mamy to, o co chodzi (a nawet więcej: okazuje się, że każda z liczb
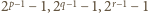 dzieli się przez iloczyn
dzieli się przez iloczyn
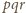 ).
).
Pozostaje wskazać liczbę pierwszą
 o podanej na wstępie własności.
Przeglądając tablicę liczb Mersenne’a znajdujemy w niej liczbę złożoną
o podanej na wstępie własności.
Przeglądając tablicę liczb Mersenne’a znajdujemy w niej liczbę złożoną
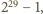 z rozkładem na czynniki pierwsze
z rozkładem na czynniki pierwsze
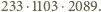 Zatem
liczby
Zatem
liczby
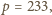
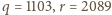 tworzą jedną z trójek, jakich
szukamy.
tworzą jedną z trójek, jakich
szukamy.
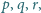 że liczba
że liczba
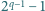 dzieli się przez
dzieli się przez
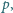 liczba
liczba
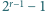 dzieli się przez
dzieli się przez
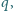 zaś liczba
zaś liczba
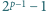 dzieli się przez
dzieli się przez
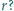

 liczba
liczba
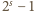 ma co
najmniej trzy różne dzielniki pierwsze
ma co
najmniej trzy różne dzielniki pierwsze
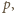
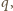
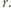 Wykażemy,
że wówczas trójka
Wykażemy,
że wówczas trójka
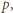
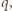
 spełnia postulowane
warunki.
spełnia postulowane
warunki.
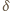 będzie najmniejszym wykładnikiem naturalnym, większym
od 1, dla którego
będzie najmniejszym wykładnikiem naturalnym, większym
od 1, dla którego
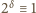 (mod
(mod
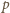 ). Z założenia także
). Z założenia także
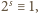 więc
więc
 dzieli się przez
dzieli się przez
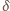 ; a skoro
; a skoro
 jest
liczbą pierwszą, to
jest
liczbą pierwszą, to
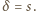 W myśl małego twierdzenia Fermata
W myśl małego twierdzenia Fermata
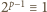 (mod
(mod
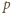 ), zatem
), zatem
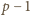 dzieli się przez
dzieli się przez
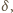 czyli
przez
czyli
przez
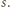
 jest dzielnikiem liczb
jest dzielnikiem liczb
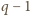 oraz
oraz
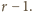 Podnosząc kongruencję
Podnosząc kongruencję
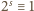 (mod
(mod
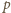 ) do potęgi
) do potęgi
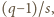 widzimy, że
widzimy, że
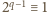 (mod
(mod
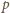 ). Tak samo,
cyklicznie,
). Tak samo,
cyklicznie,
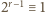 (mod
(mod
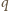 ),
),
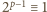 (mod
(mod
 ), czyli
mamy to, o co chodzi (a nawet więcej: okazuje się, że każda z liczb
), czyli
mamy to, o co chodzi (a nawet więcej: okazuje się, że każda z liczb
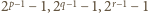 dzieli się przez iloczyn
dzieli się przez iloczyn
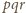 ).
).
 o podanej na wstępie własności.
Przeglądając tablicę liczb Mersenne’a znajdujemy w niej liczbę złożoną
o podanej na wstępie własności.
Przeglądając tablicę liczb Mersenne’a znajdujemy w niej liczbę złożoną
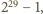 z rozkładem na czynniki pierwsze
z rozkładem na czynniki pierwsze
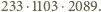 Zatem
liczby
Zatem
liczby
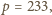
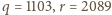 tworzą jedną z trójek, jakich
szukamy.
tworzą jedną z trójek, jakich
szukamy.