Klub 44M - zadania VI 2013»Zadanie 663
o zadaniu...
- Zadanie pochodzi z artykułu Klub 44M - zadania VI 2013
- Publikacja w Delcie: czerwiec 2013
- Publikacja elektroniczna: 28 maja 2013
- Artykuł źródłowy w wersji do druku [application/pdf]: (86 KB)
Czy istnieje nieskończony, ściśle rosnący ciąg liczb naturalnych
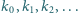 taki, że dla każdego
taki, że dla każdego
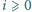 iloczyn
iloczyn
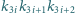 jest
podzielny przez każdą z liczb
jest
podzielny przez każdą z liczb
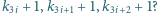

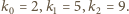 Przyjmijmy, że wyrazy
Przyjmijmy, że wyrazy
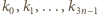 są
już określone i tworzą ciąg rosnący długości
są
już określone i tworzą ciąg rosnący długości
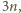 spełniający
wymagany warunek. Oznaczmy dla wygody:
spełniający
wymagany warunek. Oznaczmy dla wygody:
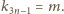 Określamy
kolejne trzy wyrazy:
Określamy
kolejne trzy wyrazy:
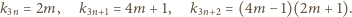
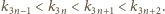 Pozostaje sprawdzić, że iloczyn
trzech wypisanych liczb, równy
Pozostaje sprawdzić, że iloczyn
trzech wypisanych liczb, równy
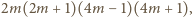 dzieli się
przez każdą z tych liczb, powiększoną o 1, czyli przez liczby
dzieli się
przez każdą z tych liczb, powiększoną o 1, czyli przez liczby
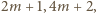
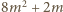 ; a to jest oczywiste. Kontynuując, otrzymujemy nieskończony
ciąg
; a to jest oczywiste. Kontynuując, otrzymujemy nieskończony
ciąg
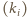 o żądanych własnościach.
o żądanych własnościach.