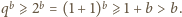O LXIII Olimpiadzie Matematycznej»Zadanie 1
o zadaniu...
- Zadanie pochodzi z artykułu O LXIII Olimpiadzie Matematycznej
- Publikacja w Delcie: lipiec 2012
- Publikacja elektroniczna: 01-07-2012
- Artykuł źródłowy w wersji do druku [application/pdf]: (69 KB)
Rozstrzygnąć, czy istnieje taka dodatnia liczba wymierna
 niebędąca
liczbą całkowitą, że potęga
niebędąca
liczbą całkowitą, że potęga
 jest liczbą wymierną
jest liczbą wymierną

 istnieje i zapiszmy ją w postaci
nieskracalnego ułamka
istnieje i zapiszmy ją w postaci
nieskracalnego ułamka
 o dodatnim liczniku i mianowniku. Dla
dowolnych liczb całkowitych
o dodatnim liczniku i mianowniku. Dla
dowolnych liczb całkowitych
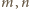 liczba
liczba
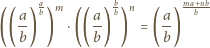
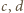
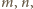
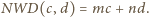
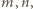 że
że
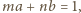 zatem
liczba
zatem
liczba
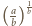 jest wymierna. Niech
jest wymierna. Niech
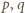 oznaczają takie względnie
pierwsze liczby naturalne, że
oznaczają takie względnie
pierwsze liczby naturalne, że
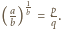 Wtedy
Wtedy
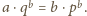 Wobec
tego, że
Wobec
tego, że
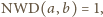 liczba
liczba
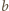 jest dzielnikiem liczby
jest dzielnikiem liczby
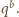 Również liczba
Również liczba
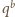 jest dzielnikiem
jest dzielnikiem
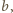 bo
bo
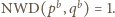 Stąd wynika, że
Stąd wynika, że
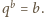 Nie jest to
możliwe, bo
Nie jest to
możliwe, bo
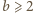 (liczba
(liczba
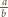 nie jest całkowita!), zatem
nie jest całkowita!), zatem