Załóżmy, że liczba
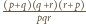 jest całkowita. Bez straty ogólności
możemy przyjąć, że
jest całkowita. Bez straty ogólności
możemy przyjąć, że
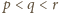 . Liczba
. Liczba
 jest pierwsza, więc musi
być dzielnikiem jednej z liczb
jest pierwsza, więc musi
być dzielnikiem jednej z liczb
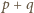 ,
,
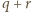 ,
,
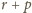 . Gdyby
liczba
. Gdyby
liczba
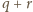 była podzielna przez
była podzielna przez
 , to przez
, to przez
 podzielna
byłaby również liczba
podzielna
byłaby również liczba
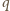 , co nie jest możliwe. Podobnie, gdyby liczba
, co nie jest możliwe. Podobnie, gdyby liczba
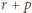 była podzielna przez
była podzielna przez
 , to przez
, to przez
 podzielna byłaby
również liczba
podzielna byłaby
również liczba
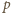 , co też nie jest możliwe. Wobec tego
, co też nie jest możliwe. Wobec tego
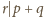 i w konsekwencji mamy
i w konsekwencji mamy
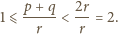
Zatem liczba
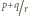 – jako liczba całkowita – musi być równa
– jako liczba całkowita – musi być równa
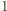 .
Stąd uzyskujemy
.
Stąd uzyskujemy
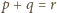 , co z kolei implikuje równość
, co z kolei implikuje równość
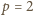 (w przeciwnym razie liczba
(w przeciwnym razie liczba
 , jako suma dwóch liczb
nieparzystych, byłaby liczbą parzystą większą od
, jako suma dwóch liczb
nieparzystych, byłaby liczbą parzystą większą od
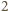 , czyli złożoną). Wobec
tego
, czyli złożoną). Wobec
tego
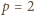 oraz
oraz
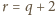 .
.
Dany w treści zadania ułamek redukuje się zatem do postaci
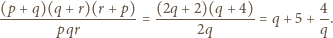
Liczba ta jest całkowita tylko wtedy, gdy
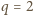 , ale wtedy
, ale wtedy
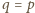 .
Otrzymujemy sprzeczność z założeniem, że liczby
.
Otrzymujemy sprzeczność z założeniem, że liczby
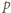 i
i
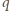 są
różne. Tak więc nie istnieją liczby
są
różne. Tak więc nie istnieją liczby
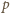 ,
,
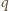 ,
,
 spełniające
warunki zadania.
spełniające
warunki zadania.
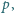
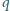 i
i
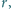 dla których
liczba
dla których
liczba
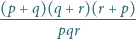

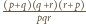 jest całkowita. Bez straty ogólności
możemy przyjąć, że
jest całkowita. Bez straty ogólności
możemy przyjąć, że
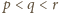 . Liczba
. Liczba
 jest pierwsza, więc musi
być dzielnikiem jednej z liczb
jest pierwsza, więc musi
być dzielnikiem jednej z liczb
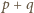 ,
,
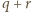 ,
,
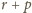 . Gdyby
liczba
. Gdyby
liczba
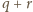 była podzielna przez
była podzielna przez
 , to przez
, to przez
 podzielna
byłaby również liczba
podzielna
byłaby również liczba
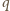 , co nie jest możliwe. Podobnie, gdyby liczba
, co nie jest możliwe. Podobnie, gdyby liczba
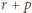 była podzielna przez
była podzielna przez
 , to przez
, to przez
 podzielna byłaby
również liczba
podzielna byłaby
również liczba
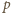 , co też nie jest możliwe. Wobec tego
, co też nie jest możliwe. Wobec tego
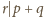 i w konsekwencji mamy
i w konsekwencji mamy
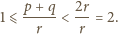
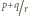 – jako liczba całkowita – musi być równa
– jako liczba całkowita – musi być równa
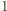 .
Stąd uzyskujemy
.
Stąd uzyskujemy
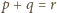 , co z kolei implikuje równość
, co z kolei implikuje równość
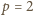 (w przeciwnym razie liczba
(w przeciwnym razie liczba
 , jako suma dwóch liczb
nieparzystych, byłaby liczbą parzystą większą od
, jako suma dwóch liczb
nieparzystych, byłaby liczbą parzystą większą od
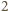 , czyli złożoną). Wobec
tego
, czyli złożoną). Wobec
tego
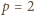 oraz
oraz
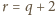 .
.
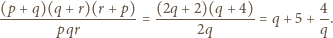
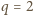 , ale wtedy
, ale wtedy
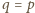 .
Otrzymujemy sprzeczność z założeniem, że liczby
.
Otrzymujemy sprzeczność z założeniem, że liczby
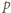 i
i
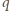 są
różne. Tak więc nie istnieją liczby
są
różne. Tak więc nie istnieją liczby
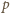 ,
,
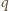 ,
,
 spełniające
warunki zadania.
spełniające
warunki zadania.