Dzieje się tak dlatego, że nasz słownik do opisu rzeczywistości jest niepełny, a własności zmieniają się w zależności od obserwacji (np. jeśli nie mamy w słowniku możliwości mówienia o młodych kaczkach, a widzimy, że takie nie latają, to pozostaje nam opisać tę rzeczywistość stwierdzeniem korzystającym z alternatywy wyrażanej za pomocą spójnika "lub": kaczka lata lub nie lata i ma skrzydła). Ujmując to symbolicznie, możemy przyjąć, że wiedzę wygodnie się zapisuje się w formacie koniunkcji alternatyw

gdzie każde z 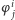jest literałem, czyli albo zdaniem atomowym (inaczej zwanym faktem), albo zaprzeczeniem zdania atomowego. Taką postać zdania logicznego nazywamy koniunkcyjną postacią normalną. Tego rodzaju wyrażenia można też zapisać w postaci

zwanej klauzulową postacią formuły, przy czym wyrażenia 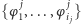nazywa się
briclink[2]klauzulami.

Wiadomo, że zapis klauzulowy ma charakter pełny - wszystkie zdania klasycznego rachunku zdań dają się równoważnie zapisać w koniunkcyjnej postaci normalnej, a więc w postaci klauzulowej.

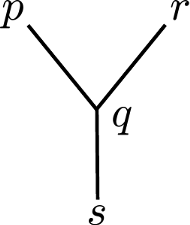
Zbudujmy teraz małą bazę faktów (którą można też nazywać bazą danych) ujętych w postaci klauzul. Ta nasza baza będzie opisywała widoczny tu obok graf złożony z czterech wierzchołków 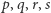oraz trzech krawędzi 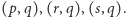Będziemy starali się w tym grafie wypatrzeć ścieżkę Hamiltona (której tam zresztą nie ma). Dla tych, którzy nie wiedzą, albo nie pamiętają: ścieżka Hamiltona to ciąg wszystkich wierzchołków grafu, w którym (1) każde kolejne wierzchołki są połączone krawędzią, (2) nie mogą występować powtórzenia. Baza będzie operowała faktami postaci 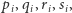które oznaczają, że odpowiedni wierzchołek znajduje się na 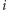-tym miejscu hipotetycznej ścieżki Hamiltona. Oto jak wygląda zawartość bazy:

(1)

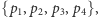
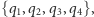
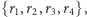
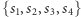
(każdy wierzchołek musi się pojawić na ścieżce),

(2)

, ,
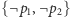
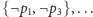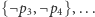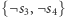
(żaden wierzchołek nie pojawia się na ścieżce dwa razy),

(3)

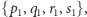
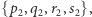
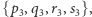
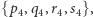
(każda pozycja na ścieżce musi być zajęta),

(4)

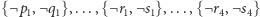
(żadne dwa różne wierzchołki nie zajmują tego samego miejsca w ciągu),

(5)

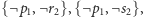
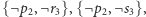
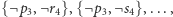
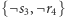
(wierzchołki niepołączone krawędzią nie mogą sąsiadować na ścieżce).

Możemy teraz pobawić się jej zawartością. Do tego wykorzystamy regułę rezolucji, która ma następującą postać:

Powyższe wzory mają następujące znaczenie: Jeśli w bazie faktów mamy dwie klauzule, z których jedna zawiera fakt, a druga jego negację, to można te klauzule połączyć, pozbywając się przy tym owego faktu i jego negacji. Nowo powstała klauzula jest dokładana do bazy. Istotę działania tej reguły łatwiej zrozumieć, jeśli uświadomimy sobie, że w logice klasycznej formuła 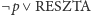jest równoważna implikacji "jeśli 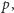to 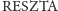". Taką właśnie postać ma pierwsza przedstawiona jawnie klauzula w regule rezolucji. Skoro zatem w drugiej klauzuli mamy w alternatywie 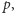to zastąpienie tegoż przez coś, co z 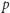wynika, powinno dać wniosek spójny z dotychczasową wiedzą.Spójne z naszym rozumieniem powyższej bazy faktów byłoby dojście do sprzeczności, która w formalizmie klauzulowym jest reprezentowana jako pusta klauzula 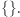Można zatem teraz postawić konkretne zadanie: jak za pomocą rezolucji dojść do bazy danych, w której będziemy mieli taką pustą klauzulę?

Gdybyśmy mieli przeprowadzić rozumowanie udowadniające brak ścieżki Hamiltonowskiej, zapewne postąpilibyśmy jakoś tak. Gdyby ścieżka zaczynała się od 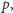wiodłaby do 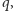a potem do lub 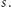W pierwszym przypadku nie moglibyśmy dojść do 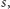w drugim nie moglibyśmy dojść do 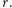Zatem ścieżka Hamiltonowska nie mogłaby się zaczynać od 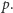Ze względu na symetrię grafu analogiczny argument zadziała dla i 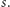Gdyby ścieżka zaczynała się od 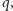to prowadziłaby po pierwszym kroku do 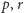lub 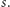W każdym z tych przypadków nie mogłaby dojść do innych wierzchołków, w szczególności odpowiednio do 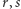i 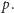Skoro rozważyliśmy wszystkie możliwe początki i dla żadnego z nich ścieżki nie było, to taka ścieżka nie istnieje.

Tego rodzaju rozumowania nie da się uprościć (zmniejszyć liczby analizowanych przypadków) za pomocą reguły rezolucji, bo nie pozwala ona na uwzględnienie symetrii. Zatem dowód z niej korzystający będzie musiał rozważyć bezpośrednio wszystkie przypadki. Jest ich dużo, spróbujmy jednak je sobie przynajmniej w części wyobrazić.

W powyższym szkicu istotne znaczenie ma sytuacja, gdy stwierdzamy, że nie może być ścieżki postaci 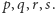Wiedza ta jest opisywana klauzulą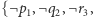 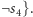Spróbujmy zobaczyć, jak ją uzyskać. Możemy wyjść z klauzuli 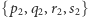z grupy (3) i użyć rezolucji z klauzulą 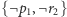z grupy (5). Uzyskamy w ten sposób 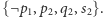Następne dwa kroki polegające na połączeniu klauzul 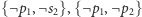z kolejnymi klauzulami wynikowymi doprowadzają nas do 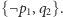Nieco inną drogą z 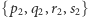dostajemy 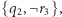zaś z 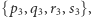klauzulę 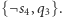Tak uzyskane trzy klauzule połączone przez rezolucję z 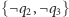z grupy (2) dadzą oczekiwane 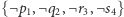(tu trzeba zwrócić uwagę, że klauzule są zbiorami, więc możemy skorzystać z trzech kopii 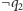w klauzuli ).

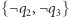Jak widać, za pomocą małych kroczków rezolucji da się wykonywać większe kroki rozumowania. Jest to żmudne i wymaga nieco pomysłowości (chwilę trzeba pomyśleć, aby zgadnąć, od której klauzuli zacząć; a tak przy okazji: ciekawą łamigłówką jest pytanie, jak dojść do klauzuli mówiących, że niemożliwe są ścieżki startujące od 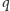; jeszcze ciekawszą - jak wykonać za pomocą przedstawionych tutaj klauzul mówiących o braku ścieżek, ostatni krok, dochodzący do sprzeczności). To wada, ale zaletą jest prostota metody - łatwo to zaprogramować. Ze żmudnością komputery jakoś sobie radzą. Stąd metoda rezolucji jest jedną z podstawowych technik w automatycznym dowodzeniu twierdzeń.