Niemożliwy skrót
Ten list uczyniłem dłuższym tylko dlatego, że nie miałem dość czasu, by napisać go krócej. Usprawiedliwienie, jakie Blaise Pascal wkłada w swój XVI List prowincjalny, wyraża intuicję, iż zapisanie jakiejś myśli zwięźle może być bardziej czasochłonne niż zapisanie jej rozwlekle. Umiejętność skrótu bywa przejawem geniuszu.
Tadeusz Boy-Żeleński odnotowuje następujący przykład sztuki translatorskiej Stanisława Wyspiańskiego. Pierwsze zdanie tragedii Pierre’a Corneille’a Cyd brzmiałoby w dosłownym przekładzie z francuskiego na polski:
Elwiro, czy zupełnie szczerze powtórzyłaś mi wszystko? Czy nie ukrywasz nic z tego, co powiedział ojciec?
W przekładzie Wyspiańskiego fragment ten brzmi
Więc mówił...?
Zostawiamy tymczasem poezję, by przyjrzeć się zagadnieniu skrótu w dziedzinie matematyki. Na przykład, jakie jest najkrótsze przedstawienie danej liczby naturalnej? Pytanie nie jest całkiem precyzyjne (co to jest przedstawienie?), ale ma pewien potencjał sensu. Jasne jest w szczególności, że odpowiedź zależy od własności danej liczby bardziej niż od jej rozmiaru. Na przykład, wypisanie cyfr dziesiętnego rozwinięcia liczby
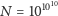
przekroczyłoby ramy tego artykułu, a nawet zapewne wszystkich numerów
Delty (dla porównania: liczbę atomów we Wszechświecie szacuje się „jedynie”
przez
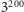 ), ale przecież przedstawiliśmy ją powyżej jednoznacznie.
W konsekwencji niedługie przedstawienie będzie miała też na pozór bardziej
skomplikowana liczba
), ale przecież przedstawiliśmy ją powyżej jednoznacznie.
W konsekwencji niedługie przedstawienie będzie miała też na pozór bardziej
skomplikowana liczba
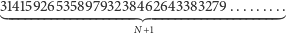
utworzona przez
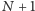 początkowych cyfr rozwinięcia dziesiętnego liczby
początkowych cyfr rozwinięcia dziesiętnego liczby
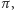 którą możemy zapisać w postaci
którą możemy zapisać w postaci
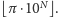 Czytelnik
zauważy oczywiście, że odwołujemy się tutaj do pewnych „kodów
kulturowych” (notacja potęgowania, definicja liczby
Czytelnik
zauważy oczywiście, że odwołujemy się tutaj do pewnych „kodów
kulturowych” (notacja potęgowania, definicja liczby
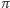 ). O tym,
że droga ta może być ryzykowna, świadczy tzw. paradoks Berry’ego
podany przez Bertranda Russella (G.G. Berry, któremu Russell przypisał
autorstwo tego paradoksu, był bibliotekarzem w oksfordzkiej Bodleian
Library):
). O tym,
że droga ta może być ryzykowna, świadczy tzw. paradoks Berry’ego
podany przez Bertranda Russella (G.G. Berry, któremu Russell przypisał
autorstwo tego paradoksu, był bibliotekarzem w oksfordzkiej Bodleian
Library):
najmniejsza liczba naturalna
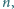 której nie da się opisać w języku
polskim przez mniej niż 1000 symboli
której nie da się opisać w języku
polskim przez mniej niż 1000 symboli
właśnie została tak opisana!
Aby uniknąć paradoksu, spójrzmy na możliwe przedstawienie liczb naturalnych
globalnie, jak na funkcję
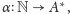 gdzie
gdzie
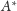 jest zbiorem
wszystkich słów, jakie można utworzyć z liter pewnego skończonego
alfabetu
jest zbiorem
wszystkich słów, jakie można utworzyć z liter pewnego skończonego
alfabetu
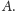 Dla jednoznaczności potrzeba, by funkcja
Dla jednoznaczności potrzeba, by funkcja
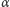 była
różnowartościowa. Interesować nas będzie długość
była
różnowartościowa. Interesować nas będzie długość
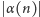 słowa
słowa
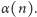 Mamy, na przykład, standardowe przedstawienia liczb w
Mamy, na przykład, standardowe przedstawienia liczb w
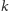 -arnym systemie pozycyjnym (np. binarnym lub dziesiętnym),
-arnym systemie pozycyjnym (np. binarnym lub dziesiętnym),
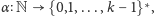 gdzie
gdzie
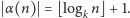 Mogłoby się
wydawać, że w każdej liczbie dopatrzymy się jakiejś „regularności”
(czyż nie uruchamiamy inwencji, by zapamiętać kod PIN?), która
pozwoli zapisać ją istotnie krócej. Jednak prosty rachunek wykaże pewną
barierę.
Mogłoby się
wydawać, że w każdej liczbie dopatrzymy się jakiejś „regularności”
(czyż nie uruchamiamy inwencji, by zapamiętać kod PIN?), która
pozwoli zapisać ją istotnie krócej. Jednak prosty rachunek wykaże pewną
barierę.
Lemat (o nieskracalności). Dla dowolnej
różnowartościowej funkcji
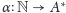 istnieje nieskończenie wiele
istnieje nieskończenie wiele
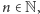 dla których
dla których
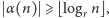 gdzie
gdzie
 jest liczbą
elementów zbioru
jest liczbą
elementów zbioru
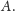
Dowód. Zauważmy najpierw, że słów krótszych niż
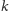 jest
jest
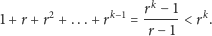
Przyjmując
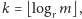 widzimy, że dla każdego
widzimy, że dla każdego
 musi
istnieć pewna liczba
musi
istnieć pewna liczba
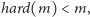 dla której
dla której
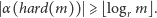
Wybierzmy najpierw
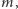 dla którego
dla którego
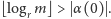 Wtedy
Wtedy
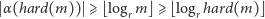
(ostatnia nierówność z nieostrej monotoniczności funkcji
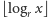 ).
Połóżmy
).
Połóżmy
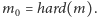 Przypuśćmy teraz, że wybraliśmy już
Przypuśćmy teraz, że wybraliśmy już
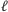 różnych liczb
różnych liczb
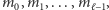 z których każda spełnia
z których każda spełnia
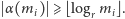 Wybierzmy
Wybierzmy
 tak, by
tak, by
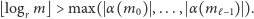 | (*) |
Ponownie, dla pewnego
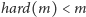 mamy
mamy
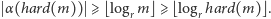 Z nierówności
Z nierówności
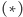 mamy
mamy
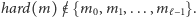 Kładziemy więc
Kładziemy więc
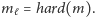
Utworzony w ten sposób ciąg
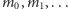 potwierdza tezę Lematu.
potwierdza tezę Lematu.
Pozwolimy sobie teraz na dygresję i pokażemy, że Lemat o nieskracalności dostarcza jednego z wielu możliwych argumentów na
Dowód. Przypuśćmy, że przeciwnie – pierwsze są jedynie
liczby
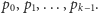 A zatem każdą liczbę naturalną można
przedstawić w postaci
A zatem każdą liczbę naturalną można
przedstawić w postaci
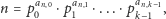
dla pewnych
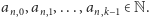 To pozwala nam określić
przedstawienie
To pozwala nam określić
przedstawienie
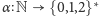
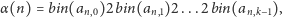
gdzie
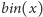 oznacza binarne przedstawienie liczby
oznacza binarne przedstawienie liczby
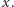 Mamy
Mamy
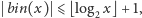 a z drugiej strony
a z drugiej strony
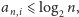 bo
bo
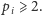 A zatem przedstawienie
A zatem przedstawienie
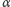 spełnia
spełnia
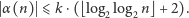
Z Lematu wynika, że dla nieskończenie wielu
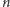
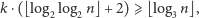
co jest, oczywiście, nie do pogodzenia z asymptotycznym zachowaniem występujących tu funkcji. A więc hipoteza skończoności zbioru liczb pierwszych była błędna.
Powróćmy do postawionego na wstępie pytania o najkrótszy opis liczby
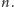 Widzieliśmy już, że każde przedstawienie ma przykłady trudno
skracalne, a z drugiej strony drastyczny skrót jest czasem możliwy.
Zauważmy jednak, że rozważanie dowolnej funkcji różnowartościowej
Widzieliśmy już, że każde przedstawienie ma przykłady trudno
skracalne, a z drugiej strony drastyczny skrót jest czasem możliwy.
Zauważmy jednak, że rozważanie dowolnej funkcji różnowartościowej
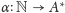 jest nieco za ogólne, oczekujemy przecież, by z przedstawienia
jest nieco za ogólne, oczekujemy przecież, by z przedstawienia
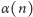 dało się odtworzyć
dało się odtworzyć
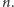 Ściślej mówiąc, interesują nas
przedstawienia
Ściślej mówiąc, interesują nas
przedstawienia
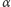 dane razem z algorytmem, który na podstawie
dane razem z algorytmem, który na podstawie
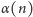 oblicza
oblicza
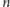 w jakimś zrozumiałym dla nas przedstawieniu
(np. dziesiętnym). W pewnym sensie
w jakimś zrozumiałym dla nas przedstawieniu
(np. dziesiętnym). W pewnym sensie
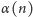 stanowi więc program, jaki
może posłużyć do obliczenia
stanowi więc program, jaki
może posłużyć do obliczenia
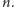 Idąc tym tropem, ustalmy sobie jakiś
język programowania (np. Pascal lub C). Zachęcamy Czytelnika, by dla
rozgrzewki napisał w swoim ulubionym języku program generujący wspomnianą
wyżej liczbę
Idąc tym tropem, ustalmy sobie jakiś
język programowania (np. Pascal lub C). Zachęcamy Czytelnika, by dla
rozgrzewki napisał w swoim ulubionym języku program generujący wspomnianą
wyżej liczbę
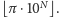 (Nie radzimy go jednak uruchamiać
(Nie radzimy go jednak uruchamiać
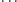 )
Ogólnie, dla dowolnej liczby
)
Ogólnie, dla dowolnej liczby
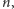 niech
niech
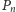 będzie programem
o najmniejszej długości, który bez żadnych dodatkowych danych generuje
liczbę
będzie programem
o najmniejszej długości, który bez żadnych dodatkowych danych generuje
liczbę
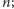 jeśli takich programów jest więcej, wybieramy pierwszy
w porządku leksykograficznym. Funkcja
jeśli takich programów jest więcej, wybieramy pierwszy
w porządku leksykograficznym. Funkcja
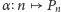 zależy wprawdzie od
wyboru języka programowania, jednak z ogólnej teorii obliczalności wynika,
że długości programów wskazywanych przez funkcje dla sensownych
języków różnią się co najwyżej o stałą (zależną od tych języków, ale nie od
zależy wprawdzie od
wyboru języka programowania, jednak z ogólnej teorii obliczalności wynika,
że długości programów wskazywanych przez funkcje dla sensownych
języków różnią się co najwyżej o stałą (zależną od tych języków, ale nie od
 ). Powyższe przedstawienie liczb naturalnych wprowadził Andriej N.
Kołmogorow w badaniach nad losowością (Kołmogorow użył jako
języka programowania abstrakcyjnego formalizmu maszyn Turinga).
Z Lematu o nieskracalności wynika bowiem, że dla nieskończenie wielu
). Powyższe przedstawienie liczb naturalnych wprowadził Andriej N.
Kołmogorow w badaniach nad losowością (Kołmogorow użył jako
języka programowania abstrakcyjnego formalizmu maszyn Turinga).
Z Lematu o nieskracalności wynika bowiem, że dla nieskończenie wielu
 jest
jest
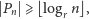
gdzie
 jest rozmiarem alfabetu, jakiego używamy w naszym języku
programowania. Można z grubsza powiedzieć, że dla takich liczb optymalnym
(lub prawie optymalnym) rozwiązaniem jest banalny program w rodzaju
write
jest rozmiarem alfabetu, jakiego używamy w naszym języku
programowania. Można z grubsza powiedzieć, że dla takich liczb optymalnym
(lub prawie optymalnym) rozwiązaniem jest banalny program w rodzaju
write
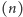 . Liczby te są „nieskracalne” z powodu braku jakiejkolwiek
regularności, a więc losowe. Funkcja
. Liczby te są „nieskracalne” z powodu braku jakiejkolwiek
regularności, a więc losowe. Funkcja
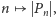 zaproponowana przez
Kołmogorowa jako miara losowości, jest dziś powszechnie nazywana
złożonością Kołmogorowa. Subtelniejsza analiza dowodu Lematu pokazuje,
że liczby trudno skracalne dominują pod względem gęstości. Paradoks polega
na tym, że trudno jest wygenerować konkretne przykłady właśnie ze względu
na losowy charakter tych liczb.
zaproponowana przez
Kołmogorowa jako miara losowości, jest dziś powszechnie nazywana
złożonością Kołmogorowa. Subtelniejsza analiza dowodu Lematu pokazuje,
że liczby trudno skracalne dominują pod względem gęstości. Paradoks polega
na tym, że trudno jest wygenerować konkretne przykłady właśnie ze względu
na losowy charakter tych liczb.
Złożoność Kołmogorowa rozwiązuje w pewnym sensie problem najkrótszego opisu, ma jednak pewną wadę, która ogranicza jej praktyczne zastosowanie. W pewnym sensie „dopada” nas tu paradoks Berry’ego.
Twierdzenie 2 (Kołmogorow). Funkcja
 jest nieobliczalna,
tzn. nie da się jej obliczyć żadnym algorytmem.
jest nieobliczalna,
tzn. nie da się jej obliczyć żadnym algorytmem.
szkic dowodu. Zakładając, że mamy taki algorytm, możemy dalej
skonstruować algorytm, który dla danego
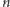 znajduje najmniejsze
znajduje najmniejsze
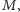 takie że
takie że
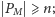 nazwijmy je
nazwijmy je
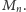
Niech
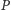 będzie
programem (z jedną zmienną wolną), który realizuje ten algorytm. Jeśli
teraz ustalimy liczbę
będzie
programem (z jedną zmienną wolną), który realizuje ten algorytm. Jeśli
teraz ustalimy liczbę
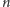 i podstawimy ją w programie
i podstawimy ją w programie
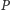 za
zmienną wolną, otrzymamy program (powiedzmy)
za
zmienną wolną, otrzymamy program (powiedzmy)
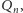 generujący
liczbę
generujący
liczbę
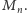 Oszacujmy jego długość. Zakładając, że
Oszacujmy jego długość. Zakładając, że
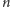 jest
dane w postaci binarnej, otrzymujemy
jest
dane w postaci binarnej, otrzymujemy
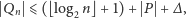
gdzie stała
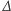 jest odpowiedzialna za podstawienie wartości
liczbowej za zmienną. (W tym miejscu odwołujemy się do składni języka
programowania.) Dla dostatecznie dużych
jest odpowiedzialna za podstawienie wartości
liczbowej za zmienną. (W tym miejscu odwołujemy się do składni języka
programowania.) Dla dostatecznie dużych
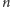 prawa strona tej
nierówności jest ostro mniejsza od
prawa strona tej
nierówności jest ostro mniejsza od
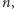 co daje nam nierówność
co daje nam nierówność
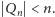 Ale założyliśmy przecież, że liczby
Ale założyliśmy przecież, że liczby
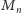 nie
da się wygenerować programem krótszym od
nie
da się wygenerować programem krótszym od
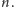 Otrzymana
sprzeczność dowodzi nieobliczalności funkcji
Otrzymana
sprzeczność dowodzi nieobliczalności funkcji
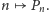
Uwaga. Czytelnik rozpoznał zapewne w powyższym rozumowaniu schemat
paradoksu Berry’ego:
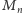 jest najmniejszą liczbą, której nie da się
wygenerować programem krótszym od
jest najmniejszą liczbą, której nie da się
wygenerować programem krótszym od
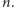 Ta liczba rzeczywiście
istnieje, nie da się jej jednak obliczyć z
Ta liczba rzeczywiście
istnieje, nie da się jej jednak obliczyć z
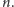
Podobne rozumowanie prowadzi do alternatywnego dowodu Twierdzenia Gödla o niezupełności, któremu poświęcony jest artykuł Wiktora Bartola Eubulides, Richard, Gödel (w tym samym numerze). Spostrzegł to Gregory Chaitin, który w tym samym czasie miał podobne idee co Kołmogorow (z tym że Kołmogorow był wtedy – w latach sześćdziesiątych XX wieku – u szczytu swojej długiej kariery, a Chaitin był jeszcze uczniem college’u). Założenia o sile wyrazu teorii są tu trochę inne, ale równie łatwe do uzyskania z prostych arytmetycznych aksjomatów.
Zakładamy mianowicie, że istnieje formuła
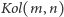 reprezentująca
relację
reprezentująca
relację
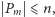 tzn. w teorii
tzn. w teorii
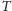 dowodzi się
dowodzi się
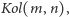 wtedy
i tylko wtedy, gdy
wtedy
i tylko wtedy, gdy
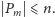
Twierdzenie 3 (Gödel–Chaitin). Jeśli teoria
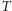 spełnia powyższe
założenie i jest niesprzeczna, to istnieje zdanie
spełnia powyższe
założenie i jest niesprzeczna, to istnieje zdanie
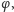 takie że ani
takie że ani
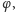 ani
ani
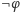 nie są twierdzeniami
nie są twierdzeniami
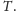
szkic dowodu.
Przypuśćmy, że nie ma takiego zdania, więc w szczególności, dla
każdej pary liczb
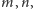 w teorii
w teorii
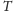 dowodzi się dokładnie
jednej z formuł
dowodzi się dokładnie
jednej z formuł
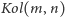 i
i
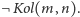 Skoro istnienie w
Skoro istnienie w
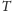 dowodu
dowodu
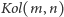 jest równoważne
jest równoważne
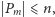 to,
wobec założonej dychotomii, istnienie w
to,
wobec założonej dychotomii, istnienie w
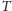 dowodu
dowodu
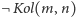 jest równoważne
jest równoważne
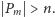
Mając dane
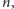 możemy więc, przeszukując wszystkie takie
dowody, znaleźć najmniejsze
możemy więc, przeszukując wszystkie takie
dowody, znaleźć najmniejsze
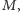 takie że
takie że
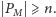 Podobnie jak poprzednio, nazwijmy je
Podobnie jak poprzednio, nazwijmy je
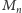 i niech
program
i niech
program
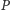 realizuje algorytm
realizuje algorytm
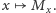 Jeśli w programie
Jeśli w programie
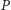 podstawimy za zmienną liczbę
podstawimy za zmienną liczbę
 w postaci binarnej, to
analogicznie jak poprzednio, znajdziemy (przy dostatecznie dużym
w postaci binarnej, to
analogicznie jak poprzednio, znajdziemy (przy dostatecznie dużym
 ) program
) program
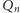 zaprzeczający definicji
zaprzeczający definicji
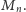
Inaczej niż w oryginalnym dowodzie Gödla, nie otrzymaliśmy tutaj
explicite konstrukcji niezależnej formuły
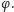 Jednak argument –
wywodzący się z paradoksu Berry’ego – jest chyba nieco prostszy i bardziej
intuicyjny, jako że odwołuje się do tempa wzrostu funkcji w miejsce
tajemniczego błędnego koła z paradoksu kłamcy. I tu, i tam widzimy, jak
paradoksy, przy odpowiedniej interpretacji, stają się konstruktywnymi
argumentami.
Jednak argument –
wywodzący się z paradoksu Berry’ego – jest chyba nieco prostszy i bardziej
intuicyjny, jako że odwołuje się do tempa wzrostu funkcji w miejsce
tajemniczego błędnego koła z paradoksu kłamcy. I tu, i tam widzimy, jak
paradoksy, przy odpowiedniej interpretacji, stają się konstruktywnymi
argumentami.