Gdy w połowie XIX wieku odkryto geometrie nieeuklidesowe, zainteresowanie matematyków zaczęło zwracać się w stronę podstaw matematyki. Na jakich podstawach można lub należy oprzeć matematykę? Na tym tle zrodził się w latach 20. XX wieku tzw. program Hilberta, postulujący zbudowanie sformalizowanej matematyki na fundamencie aksjomatycznym i wyprowadzanie z aksjomatów twierdzeń jedynie za pomocą ściśle określonych reguł. Tak zbudowana teoria powinna być zupełna i niesprzeczna i te jej własności powinny dać się udowodnić.

Teoria formalna jest zupełna, gdy każde zdanie prawdziwe w dowolnym jej modelu jest jej twierdzeniem, a więc istnieje dla niego dowód wychodzący od aksjomatów. Równoważnie, gdy dla każdego zdania 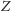 jest tak, że albo 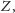 albo negacja 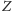 jest w tej teorii. Z kolei teoria jest niesprzeczna, gdy istnieje co najmniej jedno zdanie w jej języku, które jej twierdzeniem nie jest. Mówiąc inaczej, niesprzeczność oznacza, że nie istnieje takie zdanie 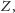 że i 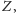  i negacja 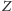 są twierdzeniami teorii.

Próbę takiej konstrukcji matematyki podjęli Brytyjczycy: Bertrand Russell i Alfred North Whitehead w publikowanym w latach 1910-1913 (choć niedokończonym) dziele Principia Mathematica. Kilkanaście lat później, w 1931 roku, ukazała się praca Kurta Friedricha Gödla Über formal unenstcheidbare Söatze der Principia Mathematica und verwandter Systeme I (O formalnie nierozstrzygalnych zdaniach Principia Mathematica i podobnych systemów). Gödel wykazał w niej, że program Hilberta nie może zostać zrealizowany: dla każdej niesprzecznej teorii matematycznej, zawierającej arytmetykę, istnieje zdanie 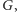 takie że ani 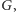 ani negacja 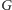 nie jest twierdzeniem tej teorii. Innymi słowy, jeśli teoria jest niesprzeczna, to nie jest zupełna.

Dwa inspirujące paradoksy

Czytelnik zapewne zetknął się ze słynnym paradoksem kłamcy, sformułowanym mniej więcej 2400 lat temu przez Eubulidesa: czy zdanie

Każda próba analizy prowadzi do nieuchronnego wniosku, że prawdziwość tego zdania jest równoważna jego fałszywości.

Wiele lat później, w 1905 roku, francuski matematyk Jules Richard sformułował inny paradoks. Wyobraźmy sobie, że dysponujemy listą wszystkich własności arytmetycznych liczb naturalnych, zapisanych w ustalonym języku naturalnym. Każdy opis własności jest skończonym ciągiem symboli ze skończonego alfabetu, zatem mamy tych własności przeliczalnie wiele, co oznacza, że możemy je ponumerować liczbami naturalnymi. W ten sposób podzieliliśmy liczby naturalne na dwie kategorie. Pierwszą niech stanowią te liczby, które mają tę własność, której są numerem. Na przykład, gdyby własność bycia liczbą parzystą miała numer 12, to 12 byłoby liczbą pierwszej kategorii, gdyż jest parzysta. Drugą kategorię niech stanowią liczby, które nie mają własności, której są numerem. Na przykład, gdyby własność bycia liczbą parzystą miała numer 5, to 5 byłoby liczbą drugiej kategorii – i te liczby nazwijmy liczbami Richarda. Bycie liczbą Richarda jest pewną własnością liczb naturalnych, został jej więc przypisany pewien numer, powiedzm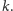y,  Czy 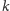 jest liczbą Richarda? Odpowiedź „tak” implikuje, że 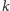 nie jest liczbą Richarda, podobnie jak odpowiedź „nie” implikuje, że nią jest. Tak więc 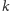 jest liczbą Richarda wtedy i tylko wtedy, gdy nią nie jest.

Pozostawiając na boku kwestię źródeł sprzeczności, odnotujmy, że w obu przypadkach mamy do czynienia ze zdaniem, które w ten czy inny sposób odnosi się samo do siebie. Co więcej, można byłoby zauważyć, że żadnego z nich nie da się ani udowodnić, ani obalić. Zauważmy jednak, że w przypadku paradoksu kłamcy mamy do czynienia z pojęciami prawdziwości i fałszywości niemieszczącymi się w żadnej teorii formalnej, w przypadku zaś paradoksu Richarda – z własnością, która zależy od kolejności, w jakiej numerujemy własności liczb naturalnych, a ta nie jest przecież własnością arytmetyczną, wyrażalną w jakiejkolwiek teorii formalnej.

Paradoksy wykorzystane

Gödel powołuje się w swojej pracy na inspiracje zaczerpnięte z powyższych paradoksów. Zasadnicza koncepcja dowodu polegała na zamianie „prawdziwości” i  „fałszywości” na „dowodliwość” i  „niedowodliwość”. Jak takie pojęcia, ściśle związane z danym systemem formalnym (w tym ze zbiorem aksjomatów, reguł wnioskowania), wyrazić w arytmetyce? 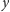Tu Gödel wpadł na pomysł, nazwany później numeracją Gödla: każdemu symbolowi (7-elementowego) alfabetu przypisał liczbę nieparzystą od 1 do 13, zmiennym reprezentującym obiekty – liczby pierwsze, poczynając od 17: zmiennej  liczbę 17, zmiennej  liczbę 19 itd. (Zmienne wyższych rzędów reprezentowane były przez potęgi liczb pierwszych). W ten sposób każdy symbol alfabetu i każda zmienna miały swój unikalny numer. Formuła jest skończonym ciągiem takich symboli. Jeśli numerami symboli kolejno występujących w formule są 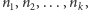 to formule przyporządkowuje się numer 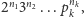 gdzie 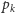 oznacza 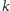 -tą liczbę pierwszą. Podobnie przypisuje się numer każdemu ciągowi formuł (a więc np. dowodom): jeśli numerami formuł są, kolejno, 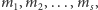 to numerem ciągu jest 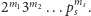 Nietrudno zauważyć, że w ten sposób każdy symbol alfabetu, każda zmienna, formuła czy ciąg formuł ma jednoznacznie przypisany numer.

Teraz należy własności systemu formalnego przetłumaczyć na język arytmetyki. Opisanie tego procesu wykracza poza możliwości tego artykułu, odnotujmy jednak dwie formuły arytmetyczne, istotne dla konstrukcji dowodu twierdzenia Gödla. 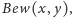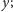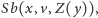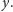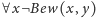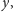Pierwsza to formuła  oznaczająca, że  jest numerem dowodu formuły o numerze  druga to formuła  reprezentująca, mówiąc w uproszczeniu, formułę powstałą przez zastąpienie w formule  zmiennej  przez  Na przykład, formuła  mówi, że żadna liczba nie jest numerem dowodu formuły o numerze  czyli – innymi słowy – formuła o numerze 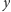 nie ma dowodu. Niech teraz  będzie numerem następującej formuły, w której dokonano pewnego podstawienia:

Przyjrzyjmy się formule (i to ona właśnie będzie zdaniem )

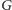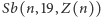 jest numerem formuły otrzymanej przez zastąpienie w formule o numerze  zmiennej o numerze 19 (czyli 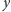 ) przez 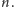 Ale to jest właśnie formuła 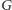 ! Mówi zatem formuła 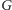 o tym, że formuła 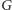 nie ma dowodu! Jak wykazuje Gödel, nie ma dowodu także jej negacja. System nie jest zupełny (przypomnijmy, jeśli jest niesprzeczny).

Tak Gödel wykorzystał twórczo oba przedstawione wyżej paradoksy. Dla pełności obrazu warto jeszcze dodać, że posługując się formułą 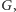 udowodnił on także, że jeśli system jest niesprzeczny, to w ramach tego systemu nie można tej niesprzeczności udowodnić. Można to zrobić w systemie obszerniejszym – pod warunkiem, że jest on niesprzeczny. Żyjemy zatem w świecie niesprzeczności warunkowej... Paradoks?