Klub 44M - zadania IX 2015»Zadanie 705
o zadaniu...
- Zadanie pochodzi z artykułu Klub 44M - zadania IX 2015
- Publikacja w Delcie: wrzesień 2015
- Publikacja elektroniczna: 31 sierpnia 2015
- Artykuł źródłowy w wersji do druku [application/pdf]: (81 KB)
Niech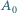 
będzie ustalonym wierzchołkiem 
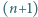-kąta foremnego. Numerujemy pozostałe wierzchołki 
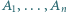w dowolnej kolejności. Każdemu bokowi 
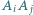przyporządkowujemy liczbę 
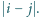Niech 
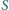będzie sumą 
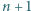liczb, przyporządkowanych wszystkim bokom. Dla zadanej liczby naturalnej 
:
- a)
- Obliczyć najmniejszą osiągalną wartość sumy
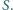
- b)
- Wyjaśnić, ile jest sposobów ponumerowania
wierzchołków (poza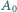 
), przy których 
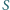osiąga ową minimalną wartość.
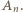Idąc od 
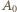do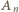 
wzdłuż brzegu wielokąta, w wybranym kierunku, mijamy kolejno wierzchołki 
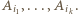Przechodzimy przez 
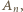dalej mijamy wierzchołki 
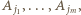i wracamy do 
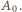Numery 
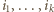oraz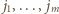 
tworzą permutację zbioru 
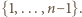Liczby, przyporządkowane wszystkim bokom, sumują się do wartości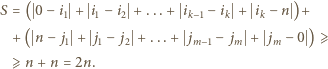
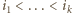oraz 
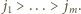Zatem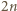 
to szukane minimum.
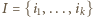może być dowolnym podzbiorem zbioru 
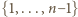(również pustym, wtedy pierwszy składnik rozpisanej sumy 
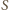ma postać 
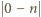). Zauważmy teraz, że już sam wybór zbioru 
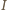determinuje ponumerowanie, realizujące równość 
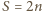; liczby ze zbioru 
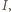uporządkowane rosnąco, trzeba przypisać kolejnym wierzchołkom (przy obieganiu wielokąta od 
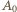w wybranym kierunku), następny wierzchołek trzeba nazwać 
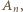a dalszym wierzchołkom dać niewykorzystane numery, uporządkowane malejąco.
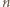wierzchołków, ile podzbiorów ma zbiór 
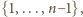to znaczy 