Kolorowe kropki»Zadanie 4
o zadaniu...
- Zadanie pochodzi z artykułu Kolorowe kropki
- Publikacja w Delcie: maj 2015
- Publikacja elektroniczna: 30-04-2015
- Artykuł źródłowy w wersji do druku [application/pdf]: (51 KB)
-
Zadanie pochodzi z obozu naukowego Olimpiady Matematycznej z 2011 roku.
Każde pole szachownicy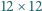 
pomalowano jednym z trzech kolorów. Wykaż, że istnieją cztery pola o tym samym kolorze, których środki są wierzchołkami prostokąta.
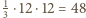pól. Rozważmy 48 pól tego właśnie koloru i niech 
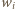oznacza liczbę tych pól występujących w 
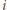-tym wierszu; oczywiście 
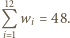W każdym wierszu dwa spośród rozważanych pól można wybrać na 
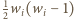sposobów. Wobec tego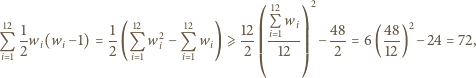
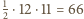sposobów - mniej niż 72. Oznacza to, że w pewnych dwóch wierszach można wybrać po dwa pola tego samego koloru i w tych samych kolumnach; ich środki tworzą szukany prostokąt.
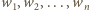zachodzi nierówność między średnią kwadratową a arytmetyczną: