Kolorowe kropki»Zadanie 1
o zadaniu...
- Zadanie pochodzi z artykułu Kolorowe kropki
- Publikacja w Delcie: maj 2015
- Publikacja elektroniczna: 30-04-2015
- Artykuł źródłowy w wersji do druku [application/pdf]: (51 KB)
Maja i Gucio grają w grę. Malują na przemian punkty płaszczyzny wedle następujących reguł. Maja rozpoczyna; w swoim ruchu maluje dowolnie wybrany bezbarwny punkt na kolorowo. Gdy nadchodzi kolej Gucia, wybiera on 2015 bezbarwnych punktów i maluje je na czarno. Maja wygrywa, jeśli na płaszczyźnie pojawią się trzy kolorowe punkty tworzące trójkąt równoboczny. Czy Gucio może jej to uniemożliwić?

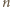 swoich ruchach Maja maluje na kolorowo
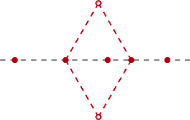
swoich ruchach Maja maluje na kolorowo 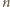 punktów z jednej prostej. Każdą parę takich kolorowych punktów można na dwa sposoby uzupełnić do trójkąta równobocznego, par punktów spośród
punktów z jednej prostej. Każdą parę takich kolorowych punktów można na dwa sposoby uzupełnić do trójkąta równobocznego, par punktów spośród  jest
jest 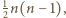 więc łącznie po
więc łącznie po 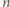 ruchach na płaszczyźnie jest
ruchach na płaszczyźnie jest 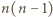 takich punktów, że pomalowanie dowolnego z nich na kolorowo da Mai zwycięstwo.
takich punktów, że pomalowanie dowolnego z nich na kolorowo da Mai zwycięstwo.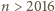 mamy
mamy 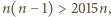 zatem Gucio nie może w swoich początkowych
zatem Gucio nie może w swoich początkowych 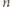 ruchach wszystkich opisanych powyżej punktów pomalować na czarno i Maja może wygrać w ruchu numer
ruchach wszystkich opisanych powyżej punktów pomalować na czarno i Maja może wygrać w ruchu numer