Klub 44M - zadania X 2013»Zadanie 667
o zadaniu...
- Zadanie pochodzi z artykułu Klub 44M - zadania X 2013
- Publikacja w Delcie: październik 2013
- Publikacja elektroniczna: 1 października 2013
- Artykuł źródłowy w wersji do druku [application/pdf]: (67 KB)
Kwadratowa plansza o rozmiarach
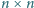 ma pola pokolorowane jak
szachownica;
ma pola pokolorowane jak
szachownica;
 jest ustaloną liczbą parzystą. Wykonujemy ciąg ruchów.
W każdym ruchu wybieramy dowolny prostokąt, złożony z pól planszy,
i zmieniamy kolory wszystkich pól w obrębie tego prostokąta (białe na czarne,
czarne na białe). Wyznaczyć najmniejszą liczbę ruchów wystarczającą, by
wszystkie pola planszy uzyskały jednakowy kolor.
jest ustaloną liczbą parzystą. Wykonujemy ciąg ruchów.
W każdym ruchu wybieramy dowolny prostokąt, złożony z pól planszy,
i zmieniamy kolory wszystkich pól w obrębie tego prostokąta (białe na czarne,
czarne na białe). Wyznaczyć najmniejszą liczbę ruchów wystarczającą, by
wszystkie pola planszy uzyskały jednakowy kolor.

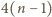 ; w stanie docelowym
wynosi 0. Jeden ruch może zmniejszyć liczbę takich par co najwyżej o 4.
Zatem liczba ruchów, po których plansza może stać się jednokolorowa, jest
nie mniejsza niż
; w stanie docelowym
wynosi 0. Jeden ruch może zmniejszyć liczbę takich par co najwyżej o 4.
Zatem liczba ruchów, po których plansza może stać się jednokolorowa, jest
nie mniejsza niż
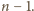
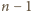 ruchów nie wystarczy do uzyskania żądanego celu, potrzeba co
najmniej
ruchów nie wystarczy do uzyskania żądanego celu, potrzeba co
najmniej
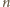 ruchów.
ruchów.
 ruchów faktycznie już wystarczy:
w początkowych
ruchów faktycznie już wystarczy:
w początkowych
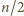 ruchach zmieniamy kolory w co drugim
wierszu, wszystkie kolumny stają się jednokolorowe (plansza „w zebrę”).
W kolejnych
ruchach zmieniamy kolory w co drugim
wierszu, wszystkie kolumny stają się jednokolorowe (plansza „w zebrę”).
W kolejnych
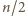 ruchach zmieniamy kolory w co drugiej kolumnie
i gotowe.
ruchach zmieniamy kolory w co drugiej kolumnie
i gotowe.