Klub 44M - zadania III 2013»Zadanie 657
o zadaniu...
- Zadanie pochodzi z artykułu Klub 44M - zadania III 2013
- Publikacja w Delcie: marzec 2013
- Publikacja elektroniczna: 1 marca 2013
- Artykuł źródłowy w wersji do druku [application/pdf]: (72 KB)
W okienka tabeli prostokątnej, mającej
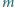 kolumn i
kolumn i
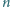 wierszy,
wpisujemy liczby
wierszy,
wpisujemy liczby
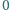 lub
lub
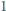 tak, by w każdym kwadracie
tak, by w każdym kwadracie
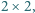 złożonym z czterech pól mających wspólny wierzchołek, suma
czterech wpisanych liczb była nieparzysta. Dla zadanej liczby naturalnej
złożonym z czterech pól mających wspólny wierzchołek, suma
czterech wpisanych liczb była nieparzysta. Dla zadanej liczby naturalnej
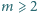 znaleźć wszystkie liczby naturalne
znaleźć wszystkie liczby naturalne
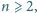 dla których da
się w taką tabelę wpisać zera i jedynki w opisany sposób tak, by żadne dwa
wiersze nie były identyczne.
dla których da
się w taką tabelę wpisać zera i jedynki w opisany sposób tak, by żadne dwa
wiersze nie były identyczne.

 Podany warunek (nieparzyste sumy w kwadratach
Podany warunek (nieparzyste sumy w kwadratach
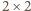 )
oznacza, że w dowolnych dwóch sąsiednich wierszach pola o numerach
parzystych są wypełnione jednakowo, a pola o numerach nieparzystych są
wypełnione różnie – lub że jest odwrotnie. Pomalujmy linię poziomą, która
te wiersze rozdziela, na szaro w pierwszym przypadku, a na żółto
w drugim.
)
oznacza, że w dowolnych dwóch sąsiednich wierszach pola o numerach
parzystych są wypełnione jednakowo, a pola o numerach nieparzystych są
wypełnione różnie – lub że jest odwrotnie. Pomalujmy linię poziomą, która
te wiersze rozdziela, na szaro w pierwszym przypadku, a na żółto
w drugim.
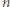 wierszy parami różnych,
wierszy parami różnych,
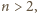 to jednakowo pomalowane linie nie mogą sąsiadować. Linie szare
i żółte występują wówczas na przemian, więc każde dwa wiersze
o numerach różniących się o 2 są wypełnione dokładnie przeciwnie
(w kolumnach, gdzie górny ma zera, dolny ma jedynki, i na odwrót).
Wobec tego wiersze o numerach różniących się o 4 są już wypełnione
identycznie.
to jednakowo pomalowane linie nie mogą sąsiadować. Linie szare
i żółte występują wówczas na przemian, więc każde dwa wiersze
o numerach różniących się o 2 są wypełnione dokładnie przeciwnie
(w kolumnach, gdzie górny ma zera, dolny ma jedynki, i na odwrót).
Wobec tego wiersze o numerach różniących się o 4 są już wypełnione
identycznie.
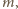 maksymalna liczba parami nieidentycznych
wierszy nie przekracza 4. Przy tym łatwo wskazać przykład takiej macierzy
z dokładnie 4 wierszami:
maksymalna liczba parami nieidentycznych
wierszy nie przekracza 4. Przy tym łatwo wskazać przykład takiej macierzy
z dokładnie 4 wierszami:
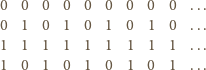
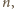 o które pyta zadanie – to 2, 3, 4.
o które pyta zadanie – to 2, 3, 4.