Cięcie chodnika długości n + k - 1 na części o długościach n oraz k - 1.

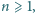
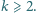
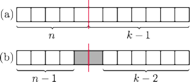
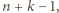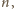Ile spośród chodników o długości  takich jak opisano w poprzednim zadaniu, można rozciąć na chodnik o długości  (od lewej strony) oraz chodnik o długości  (po prawej stronie) bez rozcinania poszczególnych płyt (Rys. (a))? Takich chodników jest tyle, na ile sposobów można ułożyć po lewej stronie chodnik długości  a po prawej chodnik długości 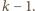  Z poprzedniego zadania wiemy, że możliwości tych jest po lewej 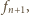 po prawej 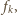 więc łącznie  Cięcie chodnika wymaga rozcinania płyty, gdy w miejscu podziału leży płyta  (Rys. (b)).

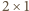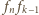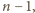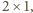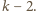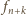Takich chodników jest : układamy od lewej kolejno chodnik długości  następnie płytę  a po prawej chodnik długości   Wszystkich chodników, jak wiemy z poprzedniego zadania, jest  i każdy z nich da się rozciąć w opisany sposób lub nie, stąd