Klub 44M - zadania III 2012»Zadanie 637
o zadaniu...
- Zadanie pochodzi z artykułu Klub 44M - zadania III 2012
- Publikacja w Delcie: marzec 2012
- Publikacja elektroniczna: 2 marca 2012
- Artykuł źródłowy w wersji do druku [application/pdf]: (68 KB)
Znaleźć wszystkie liczby naturalne
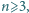 dla których zbiór
dla których zbiór
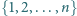 daje się przedstawić jako suma trzech rozłącznych zbiorów
o równych sumach elementów.
daje się przedstawić jako suma trzech rozłącznych zbiorów
o równych sumach elementów.

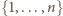 musi być podzielna przez 3 – czyli iloczyn
musi być podzielna przez 3 – czyli iloczyn
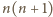 musi
dzielić się przez 6. To zaś ma miejsce jedynie dla liczb
musi
dzielić się przez 6. To zaś ma miejsce jedynie dla liczb
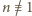 (mod 3).
Jest to więc warunek konieczny. Okazuje się, że dla
(mod 3).
Jest to więc warunek konieczny. Okazuje się, że dla
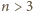 jest on też
dostateczny (jasne, że dla
jest on też
dostateczny (jasne, że dla
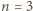 nie da się zbioru
nie da się zbioru
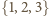 rozbić
w żądany sposób).
rozbić
w żądany sposób).
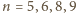 mamy, na przykład, takie rozbicia:
mamy, na przykład, takie rozbicia:
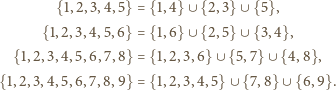
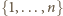 da się przedstawić jako suma trzech rozłącznych podzbiorów
o równych sumach elementów, to zbiór
da się przedstawić jako suma trzech rozłącznych podzbiorów
o równych sumach elementów, to zbiór
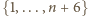 też da się tak
przedstawić – wystarczy dołączyć do pierwszego podzbioru liczby
też da się tak
przedstawić – wystarczy dołączyć do pierwszego podzbioru liczby
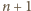 i
i
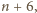 do drugiego – liczby
do drugiego – liczby
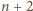 i
i
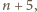 wreszcie do
trzeciego – liczby
wreszcie do
trzeciego – liczby
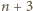 i
i
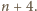 Szukanymi liczbami są więc
wszystkie liczby
Szukanymi liczbami są więc
wszystkie liczby
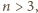 dla których
dla których
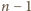 nie dzieli się
przez 3.
nie dzieli się
przez 3.